1 Introduction
Tractography is one way to represent a structural connectome, or structural network of a brain, which consists of brain regions that are physically connected by a network of neuronal bundles that make up the white matter of that brain. It is not currently possible to image individual neurons in a living brain non-invasively. Instead, we can use diffusion-weighted magnetic resonance images (DWMRI) to infer the pathways of coherent bundles of neurons that cross through other bundles in white matter and connect with end points in gray matter. There are a variety of tractography algorithms used to infer these white matter pathways, ranging from local methods that integrate local orientation information to form individual streamlines to global methods that estimate all fiber tracts simultaneously. Deterministic (Basser et al., 2000) and probabilistic (Behrens et al., 2003) streamline integration methods are easy to compute, but they suffer from accumulation of local orientation errors leading to tract reconstructions biased toward shorter and straighter tracts. Conversely, global estimation methods (Jbabdi et al., 2007; Christiaens et al., 2015) incorporate prior anatomical knowledge while ensuring that tractography is consistent with the underlying data. However, these global methods have convergence issues, sensitivity to initialization and priors, and a tendency to have estimated tracts end in the middle of white matter regions. Biases in tract reconstruction introduced by either local or global methods affect the accuracy of quantitative measures such as track density and connection strength.
Geodesic tractography algorithms, first introduced by O’Donnell et al. (2002), use a combination of local and global information to determine tracts by formulating white matter pathways as geodesic curves under a Riemannian metric derived from the DWMRI data. In the original work, O’Donnell et al. (2002) use the inverse diffusion tensor as the Riemannian metric. As described by Lenglet et al. (2004), the inverse diffusion tensor metric has a connection to Brownian motion through the Laplace Beltrami operator on the resulting Riemannian manifold. The inverse tensor metric favors paths that follow the principal eigenvector of the diffusion tensor, as this is the locally optimal direction to move. However, geodesic curves for this metric do not consistently follow the principal eigenvector of the diffusion tensor, and tend to be overly straight in regions where the white matter fibers are bending, losing association with the underlying anatomy in these areas. This problem has been addressed by several strategies to improve the adherence of geodesics to the white matter geometry, including “sharpening” the inverse diffusion tensor (Fletcher et al., 2007), using the adjugate of the diffusion tensor (Fuster et al., 2016), and using a conformal metric (Hao et al., 2014). One advantage to the geodesic tractography formulation is that we can do uncertainty and confidence interval analysis of the tractographies following (Sengers et al., 2021).
These tractography techniques help to give insight into the structure of a single brain, but it remains an open challenge to quantitatively measure how these structural connectome pathways vary in a population. To do such a population analysis, we first need a common frame of reference, or atlas space, where spatial differences between subjects’ white matter can be measured.
Initially, white matter atlases were constructed by aligning DWMRI to an anatomical template, then transforming and averaging the associated tensor field or distribution function field. For example, Mori et al. (2008) construct a diffusion tensor imaging (DTI) atlas by registering the DWMRI of multiple subjects to a standardized anatomical template. They build the DTI atlas by transforming the diffusion tensors for each subject (Alexander et al., 2001) and then taking the Euclidean average of the transformed diffusion tensors at each voxel. This approach does not use the white matter directionality information encoded in the diffusion images during the registration. It also suffers from the fact that the Euclidean average of diffusion tensors does not take into account the directionality and tends to be fatter (i.e., less anisotropic) than the input tensors (Fletcher and Joshi, 2007). Another approach by Yeh et al. (2018) is to register -space diffusion images into an anatomical template and estimate the spin distribution function (SDF) at each voxel in the template. Then the SDFs are averaged on a per-voxel basis. While this method does take into account the directionality of the white matter in a local neighborhood, it does not take into account consistency of long-range white matter connections. These methods both rely on low-accuracy registration to the anatomical template image, because at the time high-accuracy diffeomorphic registrations could not be used as they did not preserve the continuity of pathway directions across voxels (Yeh et al., 2018).
The field then focused on constructing atlases directly from tractography. These methods are adept at finding well-known tracts, but they generally require significant expert curation to remove the many false-positive fibers and tracts they create (Zhang et al., 2018). Additionally, variation of population-level tractography characteristics like fiber density of tracts is as likely to be reflective of the tractography process chosen as it is of the underlying physical white matter. These and other biases in tractography quantification are well-characterized by Jeurissen et al. (2019).
In order to get a more complete anatomical atlas, Toga et al. (2006) argue for the integrated derivation of multimodal atlases using techniques such as spatial normalization to produce more comprehensive atlases. Some attempts have been made to create a multimodal population atlas from T1 and DWMRI images. Gupta et al. (2016) rigidly register the DWMRI into the same space as the T1 template image and then apply the same deformations used to create the T1 template to the DWMRI before estimating the diffusion tensors from the transformed DWMRI. This approach puts the DWMRI and T1 images in the same space, but does not use the white matter structure to inform the creation of the T1 atlas. Other previous work on multichannel registration of diffusion and T1 MRI include Avants et al. (2007), who use a Euclidean image match metric on the diffusion tensors, and Uus et al. (2020), who use local angular correlation on the orientation distribution functions (ODFs). Like the white matter-only atlases approaches discussed above, these methods only take local information into consideration and thus do not preserve the consistency of long-range white matter connections. They do demonstrate that registration quality is improved over single channel registration when complementary channels are combined in the objective function.
We are motivated to find an approach that can preserve the best aspects of these atlas and tractography methods, while mitigating their weaknesses. Specifically, we want to create a white matter pathway atlas that preserves local orientations and other anatomical information while maintaining the continuity and integrity of long-range connections. We then want a method to bring subjects into that atlas space to enable statistical quantification of both structural connectivity and geometric variability of white matter structure across a population.
To meet these goals, we describe the metric matching framework presented by Campbell et al. (2021) in more detail and then extend it by combining diffeomorphic metric matching with diffeomorphic image matching to enable the construction of both a multimodal white and gray matter atlas simultaneously for the first time. This formulation preserves geodesics transformed by diffeomorphisms, which meets our objective to use local diffusion data and maintain the integrity of long-range connectomics as inferred by tractography (Cheng et al., 2015). We demonstrate that long-range connections are preserved by performing geodesic tractography on the resulting atlas.
1.1 Contributions of the Article
In this paper, we contribute a mathematical framework for diffeomorphic metric matching that is compatible with existing image matching frameworks to enable the creation of integrated multimodal atlases. We start by using the concept from geodesic tractography to represent connectome fibers as geodesics of a metric, that is, each brain’s white matter structure is represented as a point on the infinite-dimensional manifold of Riemannian metrics. This manifold is then equipped with the diffeomorphism-invariant Ebin metric to compute distances and geodesics between connectomes. We explain how this Riemannian manifold is the foundation for the algorithm for diffeomorphic metric registration of structural connectomes and the statistical groupwise metric atlas estimation algorithm. We then extend this model by including an image matching term in those algorithms. Finally, we simultaneously estimate an integrated multimodal white matter pathway and T1 MRI-based image atlas for the first time. This article is an extended version of the Information Processing in Medical Imaging (IPMI) conference paper (Campbell et al., 2021), where we expand the results of the conference proceedings in several major directions. Most importantly, the joint white matter pathway and T1 MRI-based image atlas model is newly introduced and, in contrast to Campbell et al. (2021) which only contained 2D examples, we now present 3D atlas construction examples.
2 Structural Connectomes as Riemannian Metrics
In the white matter of the brain, the diffusion of water is restricted perpendicular to the direction of the axons. Diffusion-weighted MRI measures the microscopic diffusion of water in multiple directions at every voxel in a 3D volume. Thus, the directionality of white matter in the brain can be locally inferred. Traditionally, global connections of the white matter have been estimated by a procedure called tractography, which numerically computes integral curves of the vector field formed by the most likely direction of fiber tracts at each point. DTI models anisotropic water diffusion with a 3x3 symmetric positive definite tensor, , at each voxel, , where the manifold is the image domain. The principal eigenvector of is aligned with the direction of the strongest diffusion.
Riemannian metrics that represent connectomics of a subject have been developed in diffusion imaging by O’Donnell et al. (2002) and include the inverse-tensor metric . However, the geodesics associated with the inverse-tensor metric tend to deviate from the principal eigenvector directions and take straighter paths through areas of high curvature.
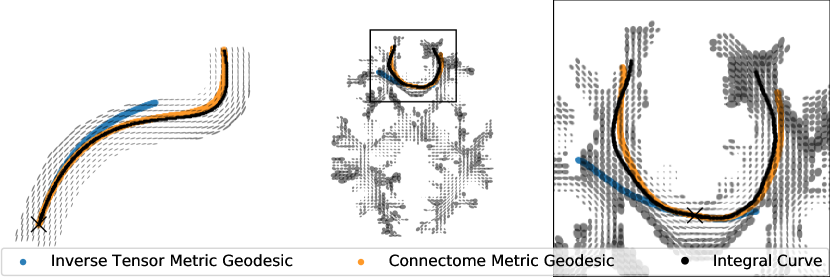
In this work we build on the algorithm developed by Hao et al. (2014), which estimates a spatially-varying function, , that modulates the inverse-tensor metric to create a locally-adaptive Riemannian metric, . We briefly describe the method here for completeness but refer the reader to Hao et al. (2014) for details. This adaptive connectome metric, , is conformally equivalent to the inverse-tensor metric and is better at capturing the global connectomics, particularly through regions of high curvature. Figure 1 shows how well the geodesics of each metric match the integral curve of the vector field. The connectome metric geodesics are very closely aligned with the integral curves.
The geodesic between two end-points, , associated with the inverse-tensor metric, , minimizes the energy functional, , while the geodesic associated with the connectome metric, , minimizes the energy functional, .
| (1) |
where , , , .
Analyzing the variation of leads to the geodesic equation, , where the Riemannian gradient of , , and is the covariant derivative of along its integral curve.
To enforce the desired condition where the tangent vectors, , of the geodesic match the vector field, , of the unit principal eigenvectors of , we minimize the functional, . The equation for that minimizes is
| (2) |
where and are the Riemannian divergence and Laplace-Beltrami operator. We discretize the Poisson equation in Equation (2) using a second-order finite difference scheme that satisfies both the Neumann boundary conditions and the governing equation on the boundary. We then solve for .
Note that we can use this method to match the geodesics of the connectome metric to other vector fields defining the tractogram, e.g., from higher-order diffusion models that can represent multiple fiber crossings in a voxel. In particular, for tractography based on fiber orientation distributions (FODs), we can use the techniques presented in Nie and Shi (2019) to generate the vector field .
The fundamental result of the purposed method is the fact that a metric tensor field is estimated such that a given vector field is a geodesic vector field of the estimated Riemannian metric. It is in this sense that the estimated metric field captures the geometry of the white matter as inferred by tractoraphy. This metric field that captures the tractography will be the primary driving force for the registration algorithms. We will now develop registration and atlas construction algorithms that leverage the rich geometric structure of Manifold of all Riemannian Metrics.
3 The Geometry of the Manifold of all Riemannian Metrics
Once we have estimated a Riemannian metric for a human connectome, it is a point in the infinite-dimensional manifold of all Riemannian metrics, , where is the domain of the image. We will equip this space with a diffeomorphism-invariant Riemannian metric, called the Ebin or DeWitt metric (Ebin, 1970; DeWitt, 1967). The invariance of the infinite-dimensional metric under the group of diffeomorphisms is a crucial property, as it guarantees the independence of an initial choice of coordinate system on the brain manifold. As we will base our statistical framework on this infinite-dimensional geometric structure, we will now give a detailed overview of its induced geometry on .
Let be a smooth -dimensional manifold; for our targeted applications will be two or three. We denote by the space of all smooth Riemannian metrics on , i.e., each element of the space is a symmetric, positive-definite tensor field on . It is convenient to think of the elements of as being point-wise positive-definite sections of the bundle of symmetric two-tensors , i.e., smooth maps from with values in . Thus, the space is an open subset of the linear space of all smooth symmetric tensor fields and hence itself a smooth Fréchet-manifold (Ebin, 1970). Furthermore, let denote the infinite-dimensional Lie group of all smooth diffeomorphisms of the manifold . Elements of act as coordinate changes on the manifold . This group acts on the space of metrics via pullback
| (3) |
In an analogous way we can define the pushforward action
| (4) |
It is important to note that the geometries of the metrics and ( resp.) are also related via . In particular, geodesics with respect to are mapped via to geodesics with respect to (via for , resp.). On the infinite-dimensional manifold , there exists a natural Riemannian metric: the reparameterization-invariant -metric. To define the metric, we need to first characterize the tangent space of the manifold of all metrics: is an open subset of . Thus, every tangent vector is a smooth bilinear form that can be equivalently interpreted as a map . The -metric is given by
| (5) |
with , and the induced volume density of the metric . This metric, introduced in Ebin (1970), is also known as the Ebin metric. We call the metric natural as it requires no additional background structure and is consequently invariant under the pushforward and pullback actions of the diffeomorphism group, i.e.,
| (6) |
for all , and . Note that the invariance of the metric follows directly from the substitution formula for multi-dimensional integrals.
The Ebin metric induces a particularly simple geometry on the space , with explicit formulas for geodesics, geodesic distance and curvature. In the following theorem and corollary, we will present the most important of these formulas, which will be of importance for our proposed metric matching framework.
First we note that a metric , in local coordinates, can be represented as a field of symmetric, positive-definite matrices that vary smoothly over . Similarly, each tangent vector at can be represented as a field of symmetric matrices. By the results of Freed et al. (1989); Gil-Medrano and Michor (1991); Clarke (2013b), one can reduce the investigations of the space of all Riemannian metrics to the study of the geometry of the finite-dimensional space of symmetric, positive-definite matrices. The point-wise nature of the Ebin metric allows one to solve the geodesic initial and boundary value problem on for each separately. Consequently the formulas for geodesics, geodesic distance and curvature on the finite-dimensional matrix space can be translated directly to results for the Ebin metric on the infinite-dimensional space of Riemannian metrics.
Note that the space of Riemannian metrics, with the Ebin metric, is not metrically complete and not geodesically convex. Thus the minimal geodesic between two Riemannian metrics may not exist in , but only in a larger space; the metric completion , which consists of all possibly degenerate Riemannian metrics. This construction has been worked out in detail by Clarke (2013a) – including the existence of minimizing paths in . In the following proof, we will omit these details and refer the interested reader to the article Clarke (2013a) for a more in-depth discussion. In Theorem 1, we present an explicit formula for the minimizing geodesic in that connects two given Riemannian metrics.
Theorem 1 (Minimizing geodesics)
For we define
| (7) | ||||
| (8) | ||||
| (9) |
Then the minimal path with respect to the Ebin metric in that connects to is given by
| (10) |
where denotes the indicator function in the variable . We suppressed the functions’ dependence on and for better readability.
Proof This theorem is essentially a reformulation of the minimal geodesic formula given in (Clarke, 2013b, Theorem 4.16). In fact, noting that the Ebin metric (5) is point-wise, we can restrict ourselves to each . By (Clarke, 2013b, Theorem 4.5), we know that in the case of , is in the image of the Riemannian exponential map starting at , and the Riemannian exponential is a diffeomorphism between and its image. Here denotes the vector space of all symmetric (0,2) tensors at . Using the formula of the inverse exponential map in (Clarke, 2013b, Theorem 4.5) we calculate the preimage of ,
| (11) |
The geodesic formula in the case of then follows immediately from (Clarke, 2013b, Theorem 4.4). For the case of , by (Clarke, 2013b, Theorem 4.14) the minimal geodesic between and is given by the concatenation of the straight segments from to the zero tensor and from the zero tensor to , which gives the last statement and finally proves the result.
An example of calculating a geodesic in the space using the explicit formula is visualized in Figure 2. The ellipse in the fifth row and fourth column, and the one in the first column and row of this figure are examples of geodesic paths that include possibly degenerate Riemannian metrics from the completion . Note that handling these degenerate cases are well understood and we did not observe any numerical issues associated with such cases.

Next, we recall that the geodesic distance of a Riemannian metric is defined as the infimum of all paths connecting two given points,
| (12) |
where the infimum is taken over all paths with and . As a direct consequence of Theorem 1, we obtain the explicit formula for the distance function given in Corollary 2.
Corollary 2 (Geodesic distance)
Let and let , , and be as in Theorem 1. Let Then the squared geodesic distance of the Ebin metric is given by
| (13) |
Proof Using Theorem 1, we obtain the formula of the minimal geodesic that connects and . By calculating the time derivative , the final statement follows from the definition of the geodesic distance (12) by a direct computation.
Having equipped the space of Riemannian metrics with the distance function (13), we can consider the Fréchet mean, , of a collection of metrics, , which is defined as a minimizer of the sum of squared distances.
| (14) |
One could directly minimize this functional using a gradient-based optimization procedure. As our distance function is the geodesic distance function of a Riemannian metric and since we have access to an explicit formula for the minimizing geodesics, we will instead use the iterative geodesic marching algorithm, see e.g. Ho et al. (2013), to approximate the Fréchet mean: Given Riemannian metrics , we approximate the Fréchet mean via , where is recursively defined as , and where is the minimal path, as given in Theorem 1, connecting to the -th data point . Thus one only has to calculate geodesics in total in the space of Riemannian metrics, whereas a gradient-based algorithm would require one to calculate geodesic distances in each step of the gradient descent.
3.1 The Induced Distance Function on the Diffeomorphism Group
We can use the geodesic distance function of the Ebin metric to induce a right-invariant distance function on the group of diffeomorphisms. As we will be using this distance function as a regularization term in our matching functional, we will briefly describe this construction here. We fix a Riemannian metric and define the “distance” of a diffeomorphism to the identity via
| (15) |
where the last equality is due to the invariance of the Ebin metric. To be more precise, this distance can be degenerate on the full diffeomorphism group since the isometries of the Riemannian metric form the kernel of . For our purposes we will consider the Euclidean metric for the definition of . Thus the only elements in the kernel are translations and rotations. The right invariance of follows directly from the -invariance of the Ebin metric. We note, however, that is not directly associated with a Riemanian structure on the diffeomorphism group: the orbits of the diffeomorphism group in the space of metrics are not totally geodesic and thus is not the geodesic distance of the pullback of the Ebin metric to the space of diffeomorphisms. See also Khesin et al. (2013) where this construction has been studied in more detail.
4 Computational Anatomy of the Human Connectome
Fundamental to the precise characterization and comparison of the human connectome of an individual subject or a population as a whole is the ability to map or register two different human connectomes. The framework of Large Deformation Diffeomorphic Metric Mapping (LDDMM) is well developed for registering points (Joshi and Miller, 2000), curves (Glaunès et al., 2008) and surfaces (Vaillant and Glaunès, 2005) all modeled as submanifolds of as well as images modeled as an function (Beg et al., 2005).This framework has also been extended to densities (Bauer et al., 2015) modeled as volume forms. We now extend the diffeomorphic mapping framework to the connectome modeled as Riemannian metrics. The diffeomorphism group deforms the domain, , and acts naturally on the space of metrics, , see Equation (4). With this action and a reparameterization-invariant metric, the problem of registering two connectomes fits naturally into the framework of computational anatomy.
Now the registration of two connectomes is achieved by minimizing the energy
| (16) |
over all such diffeomorphisms in . Here is a right invariant distance on and is a reparameterization-invariant distance on the space of all Riemannian metrics, e.g., the geodesic distance of the metrics studied above. The first term measures the deformation cost and the second term is a similarity measure between the target and the deformed source connectome. The invariance of the two distances is essential for the minimization problem to be independent of the choice of coordinate system on the brain manifold.
We use the distance function as introduced in Section 3.1 to measure the deformation cost, i.e., where is the restriction of the Euclidean metric to the brain domain. This choice greatly increases computational efficiency since we can now use the formulas from Section 3 as explicit formulas for both terms of the energy functional. To minimize the energy functional, we use a gradient flow approach described in Algorithm 1, where the gradient on is calculated with respect to a right invariant Sobolev metric of order one, which at the identity is given by
| (17) |
where is a weight parameter, is the restriction of the Euclidean metric to the brain domain and is an orthonormal basis of the harmonic vector fields on . This metric, sometimes called the information metric, has been first introduced by Modin (2015); see also Bauer et al. (2015). We choose this specific gradient because of the relation of the information metric to both the Ebin metric on the space of metrics and the Fisher-Rao metric on the space of probability densities. We summarize the relations between these geometries in Figure 3; for a precise description of the underlying geometric picture we refer to Khesin et al. (2013) and Bauer et al. (2015).
Note, that our framework allows for the immediate inclusion of points, curves, surfaces and images in the registration problem. Image intensity information, for example, can be easily incorporated in the registration problem by simply adding an appropriate similarity measure for the image term (e.g. the standard metric between the deformed moving image and the fixed image) to the energy functional. The minimization problem incorporating image intensities naturally becomes:
| (18) |
where are the relative weights and is the natural left action of Diff on images. In this convention is called the moving image ( the moving metric, resp.). It is important to note that the energy functional only depends on and not on . To see this we use the invariance of the geodesic distance on and the definition of the pushforward to rewrite (18) as
| (19) |
Consequently, we will use rather than as our optimization variable, c.f. Algorithm 1 below.
4.1 Estimating the Atlas for a Population of Connectomes
Given a collection of connectomes modeled as points on an abstract Riemannian manifold, we can directly apply least-squares estimation to define the average connectome. Thus the template estimation problem can be formulated as a joint minimization problem:
| (20) |
We use the iterative alternating algorithm proposed in Joshi et al. (2004) for solving the above optimization problem: we alternate gradient steps between optimizing with respect to each diffeomorphism, , and minimizing with respect to the metric average . In the metric optimization step we use the Fréchet mean algorithm described in Section 3. The above procedure for estimating a connectome atlas can again be trivially extended to jointly estimate an image atlas consistent with the connectome atlas. To estimate the atlases jointly we use the following extended joint minimization problem:
| (21) |
For the extended image-connectome atlas alternating algorithm at each iteration of the algorithm, the atlas image is updated by the simple average of the deformed individual subject images. This is a consequence of using the simple metric for the images. See Algorithm 2 for details of this process.
4.2 Implementation Details
In this section, we describe some implementation details that are important for reliable and efficient algorithm performance, particularly when applied to 3D brain data.
4.2.1 Metric Estimation
As done in Hao et al. (2014), we apply a mask to both the connectome metric estimation process and the atlas-building algorithm for two reasons. First, it is important that we constrain the problem to biologically realistic white matter tracts by not allowing tractography to flow through regions of CSF. Second, we avoid numeric issues associated with processing air and other noisy regions outside the skull. This also speeds up computation, as we need to look only at voxels inside the masked region instead of the entire image volume. Care must be taken with both first and second derivatives to use an appropriate and accurate finite difference stencil near the boundaries of the mask to ensure only points inside the mask are used. When matching the geodesics to a vector field consisting of the principal eigenvector directions, it is important to ensure that the eigenvector signs are consistent prior to computing derivatives of the vector field.
4.2.2 Atlas Building
For the atlas building algorithm, we deform each individual mask into atlas space at each outer iteration, and then apply the union of these deformed masks when computing the current atlas estimate. For each iteration of the atlas building algorithm, we perform only two iterations inside the metric matching function to avoid overfitting the individual metrics to early estimates of the Fréchet mean. Though we have not observed any subject order-related problems with the Fréchet mean calculation in practice, we randomize the order of the subjects each time we compute the mean to avoid the possibility of introducing problems related to subject order. In practice, we find the algorithm behaves well when we update in Algorithm 1 such that is approximately equal to the energy from (18).
For computational efficiency, all our algorithms are implemented in PyTorch, which allows us to take advantage of the built-in GPU acceleration and automatic differentiation. The computationally most expensive part in the geodesic distance of the Ebin metric is the calculation of the matrix logarithm, i.e., the calculation of . Currently the matrix logarithm function is not implemented in PyTorch, and other alternatives such as the function provided by Scipy do not support automatic differentiation. Therefore we calculate the Cholesky factorization of . We aim to use this factorization to reduce the eigendecomposition of the nonsymmetric matrix to the eigendecomposition of the symmetric matrix : writing for the eigendecomposition of , we directly obtain the eigendecomposition of , where . This in turn allows us to calculate .
Consequently, the bottleneck of our atlas building algorithm is the large amount of eigendecomposition problems that have to be computed – in each iteration step we have to solve eigendecompositions of matrices, where is the resolution of the image and is the dimension of the domain.
It turns out that the GPU implementation of torch.linalg.eig is not well-designed for solving eigendecomposition of numerous small matrices. The extremely low speed made our algorithms unusable for any experiments in 3D. To speed up these calculations, we re-implement the eigendecomposition based on the work of Lenssen et al. (2019), which leads to an order of magnitude increase in performance.
Powered by the torch.autograd module, we can now easily solve the gradient of the Ebin energy in Algorithm 1 without a closed-form gradient solution. Our 3D atlas building code, including both metric-only matching and joint matching, will become publicly available at https://github.com/aarentai/Atlas-Building-3D.
4.2.3 Geodesic Tractography
Several computational strategies have been proposed to compute white matter tractography as geodesic curves. O’Donnell et al. (2002) develop a level set approach to solve the Eikonal-type equation of the geodesic distance transform from a seed point. Fletcher et al. (2007) extend this approach to simultaneously solve for the entire set of minimal geodesics between two brain regions by solving two Hamilton-Jacobi PDEs. These Hamilton-Jacobi PDEs can be solved quickly on GPUs using the method of Jeong et al. (2007). While these strategies are better choices for a production pipeline, for this paper we chose to directly integrate the geodesic equation from seed points using the principal eigenvector at each seed as the initial direction for shooting.
Given a Riemannian metric , we compute the corresponding Christoffel symbol via
| (22) |
where denotes the components of the inverse metric tensor. Together with the position and velocity , the Christoffel symbols enable us to find the acceleration at time by solving the geodesic equation , which gives
| (23) |
where are the components of the acceleration vector and velocity vector .
After the initial conditions for the position and velocity are given and is computed, we update the acceleration at subsequent time steps using a fourth-order Runge-Kutta scheme (Press et al., 1986). See also the function algo.geodesic.geodesicpath() in our open access repository.
5 Results
We first demonstrate our framework in 2D using synthetic data and 2D data extracted from brain images. Next, we construct a 3D connectome atlas from DWMRI for a subset of subjects from the Human Connectome Project. We show that we can use the complementary information from T1-weighted MRI for those same subjects to build an integrated multimodal atlas. Finally, we demonstrate that the multimodal atlas preserves both local and long-range connectivity information by computing both whole-brain and seed region-based geodesic tractography of the atlas.
5.1 2D Simulated Data
We verified our method by generating vector fields whose central integral curves are a family of parameterized cubic functions. We used the method of parallel curves to add vectors for additional integral curves parallel to the central curve with a distance from the central curve. We then constructed tensors whose principal eigenvectors align with the generated vector fields and that have a specified major axis to minor axis ratio of 6:1.
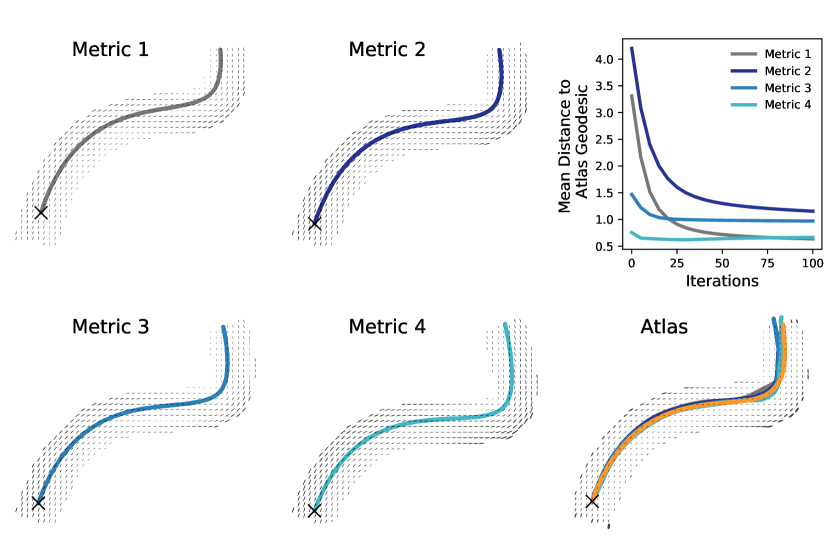
We first estimated the adaptive metric conformal to the inverse-tensor metric such that the geodesics of the adaptive metrics align with the integral curves of the simulated vector fields. After finding the connectome metric for each subject, we ran 400 iterations of the atlas building Algorithm 2 using only the metric distance as shown in (20) to estimate the atlas in Figure 4. To help the diffeomorphisms update smoothly, we set in (16) and the step size in Algorithm 1.
We compared a geodesic of the atlas starting from a particular seed point with geodesics of the four connectome metrics starting from the atlas seed point mapped into individual space. Figure 4 shows these individual geodesics in atlas space before and after applying the diffeomorphisms. We see that the atlas geodesic is nicely centered in the middle of the undeformed individual geodesics as expected. Also, the deformed individual geodesics align well with the atlas geodesic. The upper right panel shows the mean distance between the atlas geodesic and deformed subject geodesic in atlas space in different stages. After 75 iterations of optimization, we can see the distance of the four pairs of geodesics almost converged.
5.2 2D Real Data
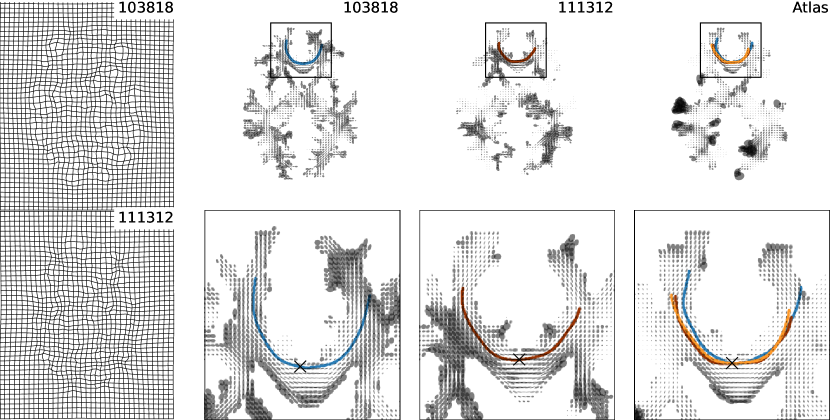
To illustrate how our method works with real data, we used two subjects from the Human Connectome Project Young Adult (HCP) dataset Glasser et al. (2013). For each subject, we fit a diffusion tensor model to the images with a -value of 1000 using dtifit from FSL Basser et al. (1994) and generated a white-matter mask based on fractional anisotropy values thresholded between 0.25 and 1. To process in 2D, we extracted a single axial slice from each image along with the x and y components of the associated tensors. We estimated the adaptive connectome metric from the inverse-tensor metric associated with the 2D diffusion tensors. We would like to emphasize that the 2D atlas construction is only for illustrative purposes. In real human data no tract is expected to live in a single plane and 2D processing is not appropriate.
To generate the atlas shown in Figure 5, we ran atlas building with only the metric distance terms from (20) for 5000 iterations with , , which took 50 minutes on an Intel Xeon Silver 4108 CPU. The regularization term, , balances the magnitudes of the diffeomorphisms from each subject’s connectome metric to the atlas. To ensure that the final geodesics in the atlas also follow the major eigenvectors of the atlas tensors, we solve for the conformal factor for the atlas as described in Section 2.
5.3 3D Metric Atlas
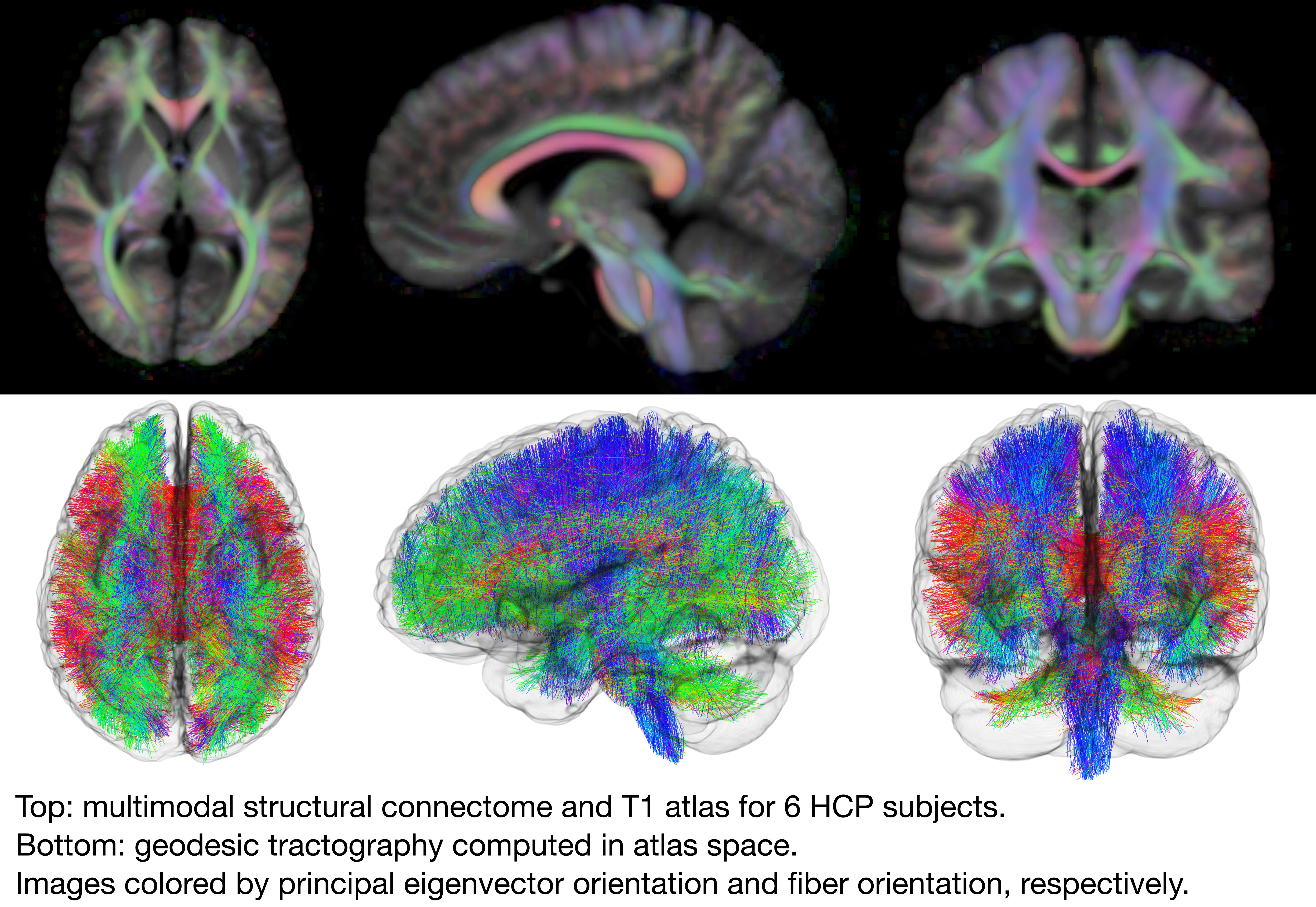
We used six subjects from the Human Connectome Project Young Adult (HCP) dataset Glasser et al. (2013) in this experiment as shown in Figure 6. For each subject, we fit a diffusion tensor model to the images using -values of 1000, 2000, and 3000 using dtifit from FSL Basser et al. (1994) and generated a white-matter mask by keeping voxels with fractional anisotropy between 0.25 and 1. We rigidly registered the T1 images for each subject using brainsfit from Johnson et al. (2007), and applied that rigid registration to the subject’s white matter mask and diffusion tensors, being sure to reorient the individual tensors. We estimated for the adaptive connectome metric from the inverse-tensor metric associated with the diffusion tensors after smoothing them with a Gaussian filter, and cleaning any tensors that were not positive semi-definite. The estimated was clipped to the range before applying it the inverse-tensor metric associated with the unsmoothed diffusion tensors to create the adaptive connectome metric. In the atlas building process, we used the metric distance terms from (20) and set the step size in Algorithm 1 and . For 800 iterations, the algorithm took about 12 hours on an Nvidia Titan RTX GPU, which features 24GB VRAM.
To generate the T1 atlas for this experiment, we computed the mean of each subject’s T1 image after deforming it by the diffeomorphism found from the metric atlas construction. As shown in Figure 7, the white matter atlas looks reasonable, but the T1 atlas is blurry, especially in gray matter regions because the atlas construction process is not using any gray matter information to guide the diffeomorphisms in these regions.
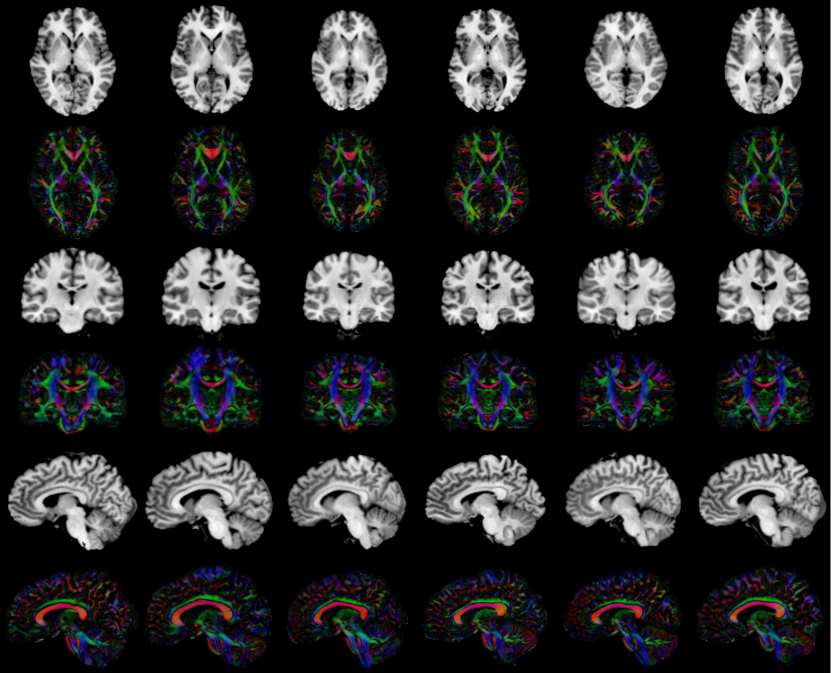
5.4 3D Joint Atlas
We used the same six subjects to construct a joint T1 and metric atlas by adding in the image matching term as shown in (21). We set the weight of the image term, in (18), to , which balances the image term loss to approximately the same magnitude as the metric term loss. All other parameters were kept the same as in the metric-only atlas building process. The resulting metric and T1 atlases are shown in Figure 7. Note how much more well-defined the gray matter regions are when the T1 information is included in the optimization process. At the same time, the metric atlas is not degraded by adding this term in, and may even be slightly better than before.
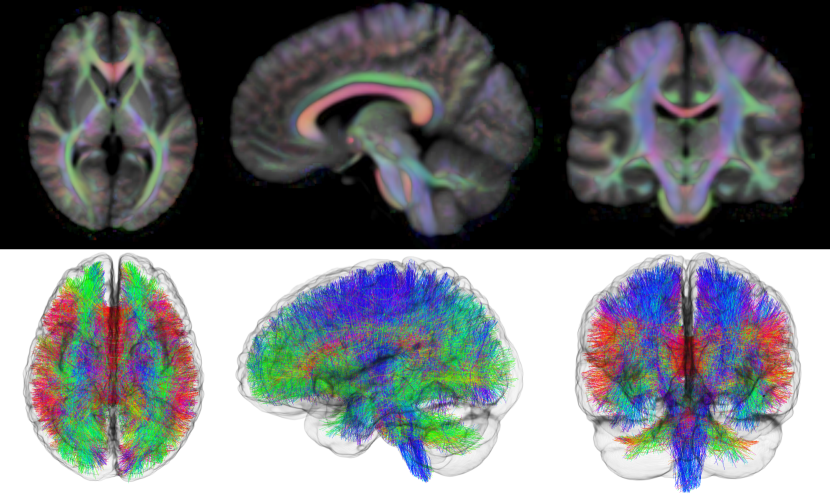
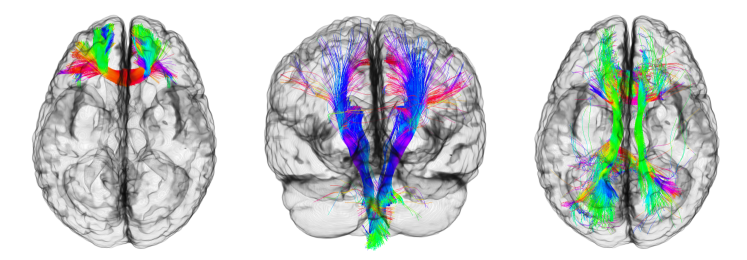
The whole-brain tractography shown in Figure 8 was performed by seeding eight geodesics per voxel in the white matter mask, stopping when each geodesic left the averaged white matter mask. Individual tracts were created by drawing seed regions in the atlas space and transforming the regions back to subject space. Each voxel in the seed region had 27 seeds. Geodesics terminated when fractional anisotropy dropped below 0.2 for the subject tractography, or when the geodesic left the averaged white matter mask for the atlas tractography. Other than the seed region and FA thresholding, we did not apply any stopping or rejection criteria based on angle, tract length, anatomical priors or any of the other techniques used to clean up false positives. We performed tractography visualization using 3D Slicer (www.slicer.org) via the SlicerDMRI project (http://dmri.slicer.org) (Norton et al., 2017; Zhang et al., 2020). Note that the whole-brain tractography can also be registered to the O’Donnell atlas using the WhiteMatterAnalysis toolkit (O’Donnell and Westin, 2007; O’Donnell et al., 2012; Zhang et al., 2018) in order to do clustering based on that atlas if desired. Example tracts for the genu of the corpus callosum, corticospinal tract, and cingulum computed by integrating geodesics of the joint atlas are shown in Figure 9.
6 Conclusions
In this paper, we introduce a novel framework for statistically analyzing structural connectomes by representing them as a point on the manifold of Riemannian metrics, enabling us to perform geometric statistics. Using this representation, we build a framework for connectome atlas construction based on the action of the diffeomorphism group and the natural Ebin metric on the space of all Riemannian metrics. Because this framework is compatible with existing image atlas construction frameworks, we are then able to construct an integrated multimodal atlas using complementary white matter and cortical information from DWMRI and T1-weighted MRI simultaneously. In future work we plan to investigate in more detail the convergence properties of the proposed algorithms and quantitatively compare our approach to other existing methods. We expect this new methodology to open up opportunities for a deeper understanding of structural connectomes, their variabilities and their relationships to cortical structure.
Acknowledgments
M. Bauer was supported by NSF grants DMS-1912037, DMS-1953244. K. Campbell, H. Dai, S. Joshi and P. Fletcher were supported by NSF grant DMS-1912030. Z. Su was supported by NSF grant DMS-1912037, NIH/NIAAA award R01-AA026834. Data were provided in part by the Human Connectome Project, WU-Minn Consortium (Principal Investigators: David Van Essen and Kamil Ugurbil; 1U54MH091657) funded by the 16 NIH Institutes and Centers that support the NIH Blueprint for Neuroscience Research; and by the McDonnell Center for Systems Neuroscience at Washington University.
Ethical Standards
The work follows appropriate ethical standards in conducting research and writing the manuscript, following all applicable laws and regulations regarding treatment of animals or human subjects.
Conflicts of Interest
The authors have no conflicts of interest.
References
- Alexander et al. (2001) Daniel C Alexander, Carlo Pierpaoli, Peter J Basser, and James C Gee. Spatial transformations of diffusion tensor magnetic resonance images. IEEE Transactions on Medical Imaging, 20(11):1131–1139, 2001.
- Avants et al. (2007) Brian Avants, Jeffrey T Duda, Hui Zhang, and James C Gee. Multivariate normalization with symmetric diffeomorphisms for multivariate studies. In International Conference on Medical Image Computing and Computer-Assisted Intervention, pages 359–366. Springer, 2007.
- Basser et al. (1994) Peter J Basser, James Mattiello, and Denis LeBihan. Estimation of the effective self-diffusion tensor from the NMR spin echo. Journal of Magnetic Resonance, Series B, 103(3):247–254, 1994.
- Basser et al. (2000) Peter J Basser, Sinisa Pajevic, Carlo Pierpaoli, Jeffrey Duda, and Akram Aldroubi. In vivo fiber tractography using DT-MRI data. Magnetic resonance in medicine, 44(4):625–632, 2000.
- Bauer et al. (2015) Martin Bauer, Sarang Joshi, and Klas Modin. Diffeomorphic density matching by optimal information transport. SIAM Journal on Imaging Sciences, 8(3):1718–1751, 2015.
- Beg et al. (2005) M Faisal Beg, Michael I Miller, Alain Trouvé, and Laurent Younes. Computing large deformation metric mappings via geodesic flows of diffeomorphisms. International Journal of Computer Vision, 61(2):139–157, 2005.
- Behrens et al. (2003) Timothy EJ Behrens, Mark W Woolrich, Mark Jenkinson, Heidi Johansen-Berg, Rita G Nunes, Stuart Clare, Paul M Matthews, J Michael Brady, and Stephen M Smith. Characterization and propagation of uncertainty in diffusion-weighted MR imaging. Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine, 50(5):1077–1088, 2003.
- Campbell et al. (2021) Kristen M Campbell, Haocheng Dai, Zhe Su, Martin Bauer, P Thomas Fletcher, and Sarang C Joshi. Structural connectome atlas construction in the space of Riemannian metrics. In International Conference on Information Processing in Medical Imaging, pages 291–303. Springer, 2021.
- Cheng et al. (2015) Guang Cheng, Hesamoddin Salehian, John R Forder, and Baba C Vemuri. Tractography from HARDI using an intrinsic unscented Kalman filter. IEEE transactions on medical imaging, 34(1):298–305, 2015.
- Christiaens et al. (2015) Daan Christiaens, Marco Reisert, Thijs Dhollander, Stefan Sunaert, Paul Suetens, and Frederik Maes. Global tractography of multi-shell diffusion-weighted imaging data using a multi-tissue model. Neuroimage, 123:89–101, 2015.
- Clarke (2013a) Brian Clarke. The completion of the manifold of Riemannian metrics. Journal of Differential Geometry, 93(2):203–268, 2013a.
- Clarke (2013b) Brian Clarke. Geodesics, distance, and the CAT(0) property for the manifold of Riemannian metrics. Mathematische Zeitschrift, 273(1-2):55–93, 2013b.
- DeWitt (1967) B. S. DeWitt. Quantum theory of gravity. I. The canonical theory. Phys. Rev., 160 (5):1113–1148, 1967.
- Ebin (1970) David G. Ebin. The manifold of Riemannian metrics. In Global Analysis (Proc. Sympos. Pure Math., Vol. XV, Berkeley, Calif., 1968), pages 11–40. Amer. Math. Soc., Providence, R.I., 1970.
- Fletcher and Joshi (2007) P Thomas Fletcher and Sarang Joshi. Riemannian geometry for the statistical analysis of diffusion tensor data. Signal Processing, 87(2):250–262, 2007.
- Fletcher et al. (2007) P Thomas Fletcher, Ran Tao, Won-Ki Jeong, and Ross T Whitaker. A volumetric approach to quantifying region-to-region white matter connectivity in diffusion tensor MRI. In Information Processing in Medical Imaging (IPMI), pages 346–358. Springer, 2007.
- Freed et al. (1989) Daniel S Freed, David Groisser, et al. The basic geometry of the manifold of Riemannian metrics and of its quotient by the diffeomorphism group. The Michigan Mathematical Journal, 36(3):323–344, 1989.
- Fuster et al. (2016) Andrea Fuster, Tom Dela Haije, Antonio Tristán-Vega, Birgit Plantinga, Carl-Fredrik Westin, and Luc Florack. Adjugate diffusion tensors for geodesic tractography in white matter. Journal of Mathematical Imaging and Vision, 54(1):1–14, 2016.
- Gil-Medrano and Michor (1991) Olga Gil-Medrano and Peter W Michor. The Riemannian manifold of all Riemannian metrics. Quarterly Journal of Mathematics (Oxford), 42:183–202, 1991.
- Glasser et al. (2013) Matthew F Glasser, Stamatios N Sotiropoulos, J Anthony Wilson, Timothy S Coalson, Bruce Fischl, Jesper L Andersson, Junqian Xu, Saad Jbabdi, Matthew Webster, and Jonathan R Polimeni. The minimal preprocessing pipelines for the human connectome project. Neuroimage, 80:105–124, 2013.
- Glaunès et al. (2008) Joan Glaunès, Anqi Qiu, Michael I Miller, and Laurent Younes. Large deformation diffeomorphic metric curve mapping. International journal of computer vision, 80(3):317, 2008.
- Gupta et al. (2016) Vikash Gupta, Grégoire Malandain, Nicholas Ayache, and Xavier Pennec. A framework for creating population specific multimodal brain atlas using clinical T1 and diffusion tensor images. In Computational Diffusion MRI, pages 99–108. Springer, 2016.
- Hao et al. (2014) Xiang Hao, Kristen Zygmunt, Ross T Whitaker, and P Thomas Fletcher. Improved segmentation of white matter tracts with adaptive Riemannian metrics. Medical Image Analysis, 18(1):161–175, 2014.
- Ho et al. (2013) Jeffrey Ho, Guang Cheng, Hesamoddin Salehian, and Baba Vemuri. Recursive Karcher expectation estimators and geometric law of large numbers. In Artificial Intelligence and Statistics, pages 325–332, 2013.
- Jbabdi et al. (2007) Saad Jbabdi, Mark W Woolrich, Jesper LR Andersson, and TEJ Behrens. A Bayesian framework for global tractography. Neuroimage, 37(1):116–129, 2007.
- Jeong et al. (2007) Won-Ki Jeong, P Thomas Fletcher, Ran Tao, and Ross Whitaker. Interactive visualization of volumetric white matter connectivity in DT-MRI using a parallel-hardware Hamilton-Jacobi solver. IEEE transactions on visualization and computer graphics, 13(6):1480–1487, 2007.
- Jeurissen et al. (2019) Ben Jeurissen, Maxime Descoteaux, Susumu Mori, and Alexander Leemans. Diffusion mri fiber tractography of the brain. NMR in Biomedicine, 32(4):e3785, 2019.
- Johnson et al. (2007) Hans Johnson, Greg Harris, Kent Williams, et al. BRAINSFit: mutual information rigid registrations of whole-brain 3D images, using the insight toolkit. Insight J, 57(1):1–10, 2007.
- Joshi et al. (2004) Sarang Joshi, Brad Davis, Matthieu Jomier, and Guido Gerig. Unbiased diffeomorphic atlas construction for computational anatomy. NeuroImage, 23:S151–S160, 2004.
- Joshi and Miller (2000) Sarang C Joshi and Michael I Miller. Landmark matching via large deformation diffeomorphisms. IEEE Transactions on Image Processing, 9(8):1357–1370, 2000.
- Khesin et al. (2013) B. Khesin, J. Lenells, G. Misiołek, and S. C. Preston. Geometry of diffeomorphism groups, complete integrability and geometric statistics. Geom. Funct. Anal., 23(1):334–366, 2013. ISSN 1016-443X.
- Lenglet et al. (2004) Christophe Lenglet, Rachid Deriche, and Olivier Faugeras. Inferring white matter geometry from diffusion tensor MRI: Application to connectivity mapping. In European Conference on Computer Vision, pages 127–140. Springer, 2004.
- Lenssen et al. (2019) Jan Eric Lenssen, Christian Osendorfer, and Jonathan Masci. Deep iterative surface normal estimation, 2019.
- Modin (2015) Klas Modin. Generalized Hunter-Saxton equations, optimal information transport, and factorization of diffeomorphisms. J. Geom. Anal., 25(2):1306–1334, 2015. ISSN 1050-6926. doi: 10.1007/s12220-014-9469-2. URL http://dx.doi.org/10.1007/s12220-014-9469-2.
- Mori et al. (2008) Susumu Mori, Kenichi Oishi, Hangyi Jiang, Li Jiang, Xin Li, Kazi Akhter, Kegang Hua, Andreia V. Faria, Asif Mahmood, Roger Woods, Arthur Toga, Bruce Pike, Pedro Rosa Neto, Alan Evans, Jiangyang Zhang, Hao Huang, Michael I. Miller, Peter van Zij, and John Mazziotta. Stereotaxic white matter atlas based on diffusion tensor imaging in an ICBM template. Neuroimage, 40(2):570–582, 2008.
- Nie and Shi (2019) Xinyu Nie and Yonggang Shi. Topographic filtering of tractograms as vector field flows. In International Conference on Medical Image Computing and Computer-Assisted Intervention, pages 564–572. Springer, 2019.
- Norton et al. (2017) Isaiah Norton, Walid Ibn Essayed, Fan Zhang, Sonia Pujol, Alex Yarmarkovich, Alexandra J Golby, Gordon Kindlmann, Demian Wassermann, Raul San Jose Estepar, Yogesh Rathi, et al. SlicerDMRI: open source diffusion MRI software for brain cancer research. Cancer research, 77(21):e101–e103, 2017.
- O’Donnell et al. (2002) Lauren O’Donnell, Steven Haker, and Carl-Fredrik Westin. New approaches to estimation of white matter connectivity in diffusion tensor MRI: Elliptic PDEs and geodesics in a tensor-warped space. In International Conference on Medical Image Computing and Computer-Assisted Intervention, pages 459–466, 2002.
- O’Donnell and Westin (2007) Lauren J O’Donnell and Carl-Fredrik Westin. Automatic tractography segmentation using a high-dimensional white matter atlas. IEEE transactions on medical imaging, 26(11):1562–1575, 2007.
- O’Donnell et al. (2012) Lauren J O’Donnell, William M Wells, Alexandra J Golby, and Carl-Fredrik Westin. Unbiased groupwise registration of white matter tractography. In International Conference on Medical Image Computing and Computer-Assisted Intervention, pages 123–130. Springer, 2012.
- Press et al. (1986) William H Press, William T Vetterling, Saul A Teukolsky, and Brian P Flannery. Numerical recipes, volume 818. Cambridge university press Cambridge, 1986.
- Sengers et al. (2021) Rick Sengers, Luc Florack, and Andrea Fuster. Geodesic tubes for uncertainty quantification in diffusion MR. In Information Processing in Medical Imaging (IPMI), pages 279–290. Springer, 2021.
- Toga et al. (2006) Arthur W Toga, Paul M Thompson, Susumu Mori, Katrin Amunts, and Karl Zilles. Towards multimodal atlases of the human brain. Nature Reviews Neuroscience, 7(12):952–966, 2006.
- Uus et al. (2020) Alena Uus, Maximilian Pietsch, Irina Grigorescu, Daan Christiaens, Jacques-Donald Tournier, Lucilio Cordero Grande, Jana Hutter, David Edwards, Joseph Hajnal, and Maria Deprez. Multi-channel registration for diffusion MRI: Longitudinal analysis for the neonatal brain. In International Workshop on Biomedical Image Registration, pages 111–121. Springer, 2020.
- Vaillant and Glaunès (2005) Marc Vaillant and Joan Glaunès. Surface matching via currents. In International Conference on Information Processing in Medical Imaging, pages 381–392. Springer, 2005.
- Yeh et al. (2018) Fang-Cheng Yeh, Sandip Panesar, David Fernandes, Antonio Meola, Masanori Yoshino, Juan C Fernandez-Miranda, Jean M Vettel, and Timothy Verstynen. Population-averaged atlas of the macroscale human structural connectome and its network topology. NeuroImage, 178:57–68, 2018.
- Zhang et al. (2018) Fan Zhang, Ye Wu, Isaiah Norton, Laura Rigolo, Yogesh Rathi, Nikos Makris, and Lauren J O’Donnell. An anatomically curated fiber clustering white matter atlas for consistent white matter tract parcellation across the lifespan. NeuroImage, 179:429–447, 2018.
- Zhang et al. (2020) Fan Zhang, Thomas Noh, Parikshit Juvekar, Sarah F Frisken, Laura Rigolo, Isaiah Norton, Tina Kapur, Sonia Pujol, William Wells III, Alex Yarmarkovich, et al. SlicerDMRI: Diffusion MRI and tractography research software for brain cancer surgery planning and visualization. JCO clinical cancer informatics, 4:299–309, 2020.