BrainMorph: A Foundational Keypoint Model for Robust and Flexible Brain MRI Registration

Wang, Alan Q.; Saluja, Rachit; Kim, Heejong; He, Xinzi; Dalca, Adrian; Sabuncu, Mert R.

doi:https://doi.org/10.59275/j.melba.2025-59g7

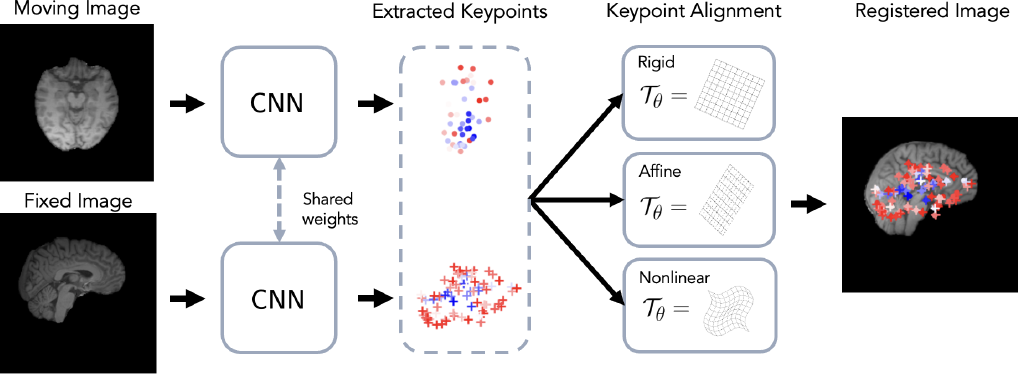
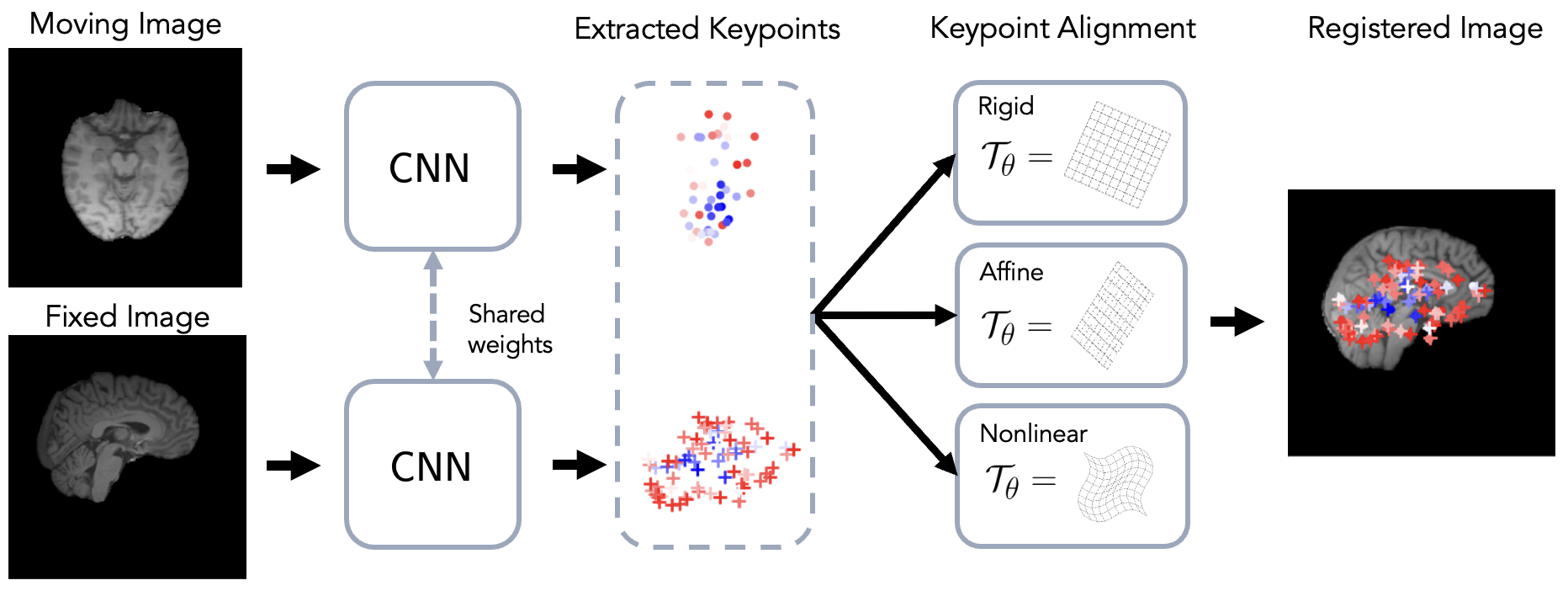
1 Introduction

Registration is a fundamental problem in biomedical imaging tasks. Multiple images, often reflecting a variety of contrasts, modalities, subjects, and underlying pathologies, are commonly acquired in many applications (Uludağ and Roebroeck, 2014). Registration seeks to spatially align these images in order to facilitate downstream analyses, like tracking longitudinal changes, studying disease progression, or analyzing population-level variability.

Refer to caption — Figure 1: The framework of BrainMorph. Fixed and moving 3D brain images are passed through the same keypoint detection network, which predicts $N$ keypoints useful for registration. The transformation parameters are then computed as a function of the keypoints, which are in turn used to resample the moving image. Keypoint colors denote depth (see Fig. 2).

Registration can be broken down into different types. It may be performed within the same modality (unimodal) or across different modalities (multimodal). Pairwise registration performs registration on an image pair, while groupwise registration performs registration on multiple images at once (Guyader et al., 2018). To perform the registration, various families of spatial transformations can be used, including rigid, affine, and nonlinear transformations.

Different lines of research have been explored to solve the registration task. “Classical” (i.e. non-learning-based) registration methods solve an iterative optimization of a similarity metric over a space of transformations, with additional regularization terms that restrict the space of plausible transformations (Oliveira and Tavares, 2014; Sotiras et al., 2013). Much research is dedicated to developing good transformations, similarity metrics, and optimization strategies. While performant, these approaches are known to suffer from long run times, often requiring upwards of several minutes to register a pair of images. In addition, these approaches are known to perform poorly when the initial misalignment between images is large (e.g. 90 degrees of rotational misalignment).

Another line of work decomposes the registration problem into two steps. First, salient features (e.g. keypoints or contours) are extracted from images, and correspondences are established between the features of the image pair. Second, the transformation is derived which aligns these features and correspondences. In this work, we refer to methods that extract keypoints as salient features as “keypoint-based” registration. Largely, keypoint-based registration is advantageous in that the registration is relatively robust to initial misalignments, given good correspondences. In addition, these methods enjoy superior interpretability, because the user can interrogate the correspondences which are driving the registration. However, finding keypoints and establishing correspondences is a difficult task and is a subject of much research (Lowe, 2004; Tang et al., 2023, 2019).

More recently, deep learning-based strategies have emerged which leverage large datasets of images to train a neural network to perform the registration task. These strategies use convolutional neural network (CNN) or transformer-based architectures (Ma et al., 2022; Chen et al., 2021; Khan et al., 2021) that either output transformation parameters (e.g. rigid, affine or spline) (Lee et al., 2019a; de Vos et al., 2019) or a dense deformation field (Balakrishnan et al., 2019; Hoffmann et al., 2022) which aligns an image pair. These strategies are effective and are able to perform fast inference via efficient feed-forward passes. However, they often fail when the initial misalignment is large and are usually less robust than their classical counterparts.

Recently, the KeyMorph framework proposed to combine the benefits of keypoint-based registration with deep learning using neural networks to automatically detect corresponding keypoints (Yu et al., 2022; Wang et al., 2023). Corresponding keypoints can then be used to compute the optimal transformation in closed-form, where the keypoints themselves are learned by a neural network. Thus, KeyMorph may be seen as possessing all the benefits of keypoint-based registration, including robustness to large misalignments and better interpretability, while retaining the fast inference times of deep learning-based methods. In addition, different transformation can be used according to user specifications, thereby enabling human controllability of the registration process.

In this work, we extend the KeyMorph framework into a general-purpose tool for brain MRI registration. Although the literature on deep-learning-based registration methods has been widely explored and many tools exist with support for brain MRIs (Avants et al., 2008b; Konstantinos Ntatsis et al., 2023; Hoffmann et al., 2022), most works focus on cross-subject pairwise registration on healthy subjects with skull-stripped images. Groupwise registration and support for non-skull-stripped and diseased subjects is often ignored, or is prohibitively slow or memory-intensive (Konstantinos Ntatsis et al., 2023). Often, the tools that do exist require time-consuming preprocessing steps like skullstripping and pre-affine registration (Balakrishnan et al., 2019; Hoffmann et al., 2022). In short, there is a lack of software tools for brain MRIs which is capable of supporting registration across a wide swath of use cases, including healthy and diseased subjects, pairwise/longitudinal/groupwise registration, and minimal assumptions on preprocessing (like skullstripping).

We refer to our proposed tool as BrainMorph. BrainMorph is a tool built on the KeyMorph framework that is trained on a massive dataset of over 100,000 volumes consisting of both skull-stripped and non-skull-stripped data of diseased and normal subjects in a variety of MRI modalities. Our tool supports rigid, affine, and nonlinear registration. In addition to pairwise registration, we introduce a novel and memory-efficient approach to groupwise registration and demonstrate the superiority and scalability of our approach in population-level and longitudinal settings. All code and models are available at:
https://github.com/alanqrwang/brainmorph.

This work builds on previous works on KeyMorph (Yu et al., 2022; Wang et al., 2023) in the following ways:

1.
We scale up training of the KeyMorph framework on a massive dataset of over 100,000 volumes at 1mm isotropic resolution, enabling our resulting model to be robust to full-resolution skull-stripped and non-skull-stripped data, a variety of MRI modalities, and diseased and normal subjects.
2.
We introduce a groupwise registration algorithm operating on the learned keypoints that is scalable and memory efficient.
3.
We provide code and all model variants such that our models can be used as a tool for the research community.

2 Background

Classical Methods. Pairwise iterative, optimization-based approaches have been extensively studied in medical image registration (Hill et al., 2001; Oliveira and Tavares, 2014). These methods employ a variety of similarity functions, types of deformation, transformation constraints or regularization strategies, and optimization techniques. Intensity-based similarity criteria are most often used, such as mean-squared error (MSE) or normalized cross correlation for registering images of the same modality (Avants et al., 2009, 2008a; Hermosillo et al., 2002). For registering image pairs from different modalities, statistical measures like mutual information or contrast-invariant features like MIND are popular (Heinrich et al., 2012; Hermosillo et al., 2002; Hoffmann et al., 2021; Mattes et al., 2003; Viola and Wells III, 1997).

Keypoint-based Methods. Another registration paradigm first detects features or keypoints in the images, and then establishes their correspondence. This approach often involves handcrafted features (Tuytelaars and Mikolajczyk, 2008), features extracted from curvature of contours (Rosenfeld and Thurston, 1971), image intensity (Förstner and Gülch, 1987; Harris et al., 1988), color information (Montesinos et al., 1998; Van de Weijer et al., 2005), or segmented regions (Matas et al., 2004; Wachinger et al., 2018). Features can be also obtained so that they are invariant to viewpoints (Bay et al., 2006; Brown et al., 2005; Lowe, 2004; Toews et al., 2013a). These algorithms then optimize similarity functions based on these features over the space of transformations (Chui and Rangarajan, 2003; Hill et al., 2001). This strategy is sensitive to the quality of the keypoints and often suffer in the presence of substantial contrast and/or color variation (Verdie et al., 2015).

Deep Learning-based Methods. In learning-based image registration, supervision can be provided through ground-truth transformations, either synthesized or computed by classical methods (Cao et al., 2018; Dosovitskiy et al., 2015; Eppenhof and Pluim, 2018; Lee et al., 2019b; Uzunova et al., 2017; Yang et al., 2017). Unsupervised strategies use loss functions similar to those employed in classical methods (Balakrishnan et al., 2019; Dalca et al., 2019; de Vos et al., 2019; Fan et al., 2018; Krebs et al., 2019; Qin et al., 2019; Wu et al., 2015; Hoopes et al., 2021). Weakly supervised models employ (additional) landmarks or labels to guide training (Balakrishnan et al., 2019; Fan et al., 2019; Hu et al., 2018a, b).

Recent learning-based methods compute image features or keypoints (Ma et al., 2021; Moyer et al., 2021) that can be used for image recognition, retrieval, tracking, or registration. Learning useful features or keypoints can be done with supervision (Verdie et al., 2015; Yi et al., 2016, 2018), self-supervision (DeTone et al., 2018; Liu et al., 2021) or without supervision (Barroso-Laguna et al., 2019; Lenc and Vedaldi, 2016; Ono et al., 2018). Finding correspondences between pairs of images usually involves identifying the learned features which are most similar between the pair. In contrast, our method uses a single network which extract/generates corresponding keypoints directly from both the moving and fixed image. The keypoints between the moving and fixed image are guaranteed to be in correspondence, since one network extracts keypoints from both images. We optimize these corresponding keypoints directly for the registration task (and not using any intermediate keypoint supervision).

Model	CPU Time, pre-processed	GPU Time, pre-processed	CPU Time, raw	GPU Time, raw
ANTs, Rigid	101.38 $\pm$ 2.33	-	143.38 $\pm$ 2.33	-
ANTs, Affine	110.45 $\pm$ 2.94	-	142.45 $\pm$ 2.94	-
ANTs, Syn	216.03 $\pm$ 3.14	-	248.03 $\pm$ 3.14	-
BrainMorph, Rigid	109.84 $\pm$ 1.80	1.05 $\pm$ 0.29	108.27 $\pm$ 1.82	1.05 $\pm$ 0.25
BrainMorph, Affine	109.63 $\pm$ 1.84	1.04 $\pm$ 0.36	110.31 $\pm$ 1.90	1.05 $\pm$ 0.32
BrainMorph, TPS	180.14 $\pm$ 1.99	1.24 $\pm$ 0.30	180.40 $\pm$ 1.91	1.25 $\pm$ 0.31

Table 1: Average computation time in seconds for pairwise registration across different models. We separate between times when performing registration with pre-processed data and raw data. For ANTs, pre-processing requires skull-stripping with HD-BET, which adds an additional 32 seconds (Isensee et al., 2019). For SynthMorph, pre-processing requires an initial robust affine registration into a reference space. BrainMorph timings are based on BrainMorph-L. Note: all times are inference times. BrainMorph requires about 5 days of training time (compute details in Sec. 4.2), while ANTs does not.

Learning-based methods for multi-modal registration are of great practical utility and often-studied in the literature. Most works require, in addition to the moving and fixed image, a corresponding image in a standard space which can be compared and which drives the alignment, usually in the form of segmentations. (Zhang et al., 2022) address multi-modal retinal images and handle multi-modality by transforming each image to a standard grayscale image via vessel segmentation. A standard feature detection and description procedure is used to find correspondences from these standard images. Other works (Song et al., 2022) rely on segmentations from ultrasound and magnetic resonance images to align them. Obtaining these segmentations may be costly, add additional computational complexity to the registration procedure, or be specific to the anatomies/modalities in question. In contrast, our method can be applied generally to any registration problem. In addition, we present a variant of our model which only relies on the images themselves during training. In our experiments, we find that this variant outperforms state-of-the-art baselines while also performing comparably to a variant of our model which leverages segmentations.

3 BrainMorph

Our tool, BrainMorph, is based on the previously published KeyMorph framework and we refer the reader to prior papers for more details (Yu et al., 2022; Wang et al., 2023). Let $(\bm{x}_{m},\bm{x}_{f})$ be a moving (source) and fixed (target) image¹¹1Although we consider 3D volumes in this work, BrainMorph is agnostic to the number of dimensions. The terms “image” and “volume” are used interchangeably. pair, possibly of different contrasts or modalities. Additionally, we denote by $\mathcal{T}_{\theta}$ a parametric coordinate transformation with parameters $\theta$ , such as those discussed in B. The goal is to find the optimal transformation $\mathcal{T}_{\theta^{*}}$ such that the registered image $\bm{x}_{r}=\bm{x}_{m}\circ\mathcal{T}_{\theta^{*}}$ aligns with some fixed image $\bm{x}_{f}$ , where $\circ$ denotes the spatial transformation of an image.

BrainMorph works by detecting $N$ keypoints $\bm{P}\in\mathbb{R}^{D\times N}$ from any given image. In this work, $D=3$ . The keypoints are detected by a neural network $f_{\psi}$ . Since a single $f_{\psi}$ detects keypoints for any image and the detected keypoints are used to optimize a registration objective (see Section 3.2), the keypoints for any arbitrary image pair are in correspondence. Given corresponding keypoint sets $\bm{P}$ and $\bm{Q}$ , the optimal transformation can be derived using a keypoint solver, which outputs the optimal transformation parameters as a function of the keypoints: $\theta^{*}(\bm{P},\bm{Q},\bm{w})$ . Here, we optionally include as arguments a vector of weights $\bm{w}$ which weight the correspondences, such that lower weights lead to a lower contribution to the overall alignment. Further details are given in Section 4.3.

Fig. 1 depicts a graphical overview of BrainMorph. Note this formulation unlocks the benefits of keypoint-based registration, including robustness to large misalignments and interpretability (as compared to other learning-based methods) via visualizing the keypoints. Moreover, this formulation enables controllability in the sense that different transformations can be used to align the keypoints. In particular, during training, this allows for heterogeneity in training, such that the model can be robust to a wide variety of transformation types. At test-time, one can generate a dense set of registrations; the controllable nature of this framework enables the user to select the preferred registration.

3.1 Keypoint Detection Network

BrainMorph can leverage any deep learning-based keypoint detector (Ma et al., 2021; DeTone et al., 2018; Barroso-Laguna et al., 2019). In this work, we use a UNet-style architecture which takes in a single channel image and outputs $N$ feature maps. We are interested in preserving translation equivariance; to this end, we leverage a center-of-mass (CoM) layer (Ma et al., 2020; Sofka et al., 2017) as the final layer, which computes the center-of-mass for each of the $N$ activation maps. This specialized layer is (approximately) translationally-equivariant and enables precise localization. Since the CoM layer expects positive values at every grid location, we insert a ReLU activation before the CoM layer.

3.2 Training

Training BrainMorph involves optimizing the learnable parameters within the CNN $f_{\psi}$ for pairwise registration. During training, we randomly sample pairs of moving and fixed images, and the general objective is:

\displaystyle\begin{split}\operatorname*{arg\,max}_{\psi}\ &\mathbb{E}_{(\bm{x}_{m},\bm{x}_{f})}\ \mathcal{L}_{sim}\left(\bm{x}_{m}\circ\mathcal{T}_{\theta^{*}},\bm{x}_{f}\right)\\ &\text{where }\ \ \theta^{*}=\theta^{*}\left(f_{\psi}(\bm{x}_{f}),f_{\psi}(\bm{x}_{m}),\bm{w}\right)\end{split}

(1)

where $\mathcal{L}_{sim}(\cdot,\cdot)$ measures image similarity between its two inputs. Weights $\bm{w}$ for keypoints correspondences are found as follows. First, we compute the energy (i.e. the aggregated sum) of each of the $N$ activation maps for both the fixed and moving image. Then, we multiply the corresponding energies, and compute the softmax of the $N$ energies to arrive at normalized weights (Moyer et al., 2021).

In this work, we choose transformations whose optimal parameters can be solved in a closed-form and differentiable manner so that $f_{\psi}$ can be trained in an end-to-end fashion. Thus, the neural network is incentivized to detect $N$ anatomically-consistent keypoints from a given image, such that a good registration can be achieved. Note that we do not rely on any ground truth keypoints as supervision.

The BrainMorph framework enables flexibility in training depending on the choice of the loss function and the transformation used. $\mathcal{L}_{sim}$ can be any similarity function and can vary during training depending on the image pairs. In this work, we use MSE or Dice loss, depending on the current image pair. The closed-form optimal solution $\theta^{*}$ can depend on a hyperparameter $\lambda$ , such as in TPS, which can be set to a constant or sampled from a distribution $\lambda\sim p(\lambda)$ during training. More details on the training details we used in this work are presented in Section 4.2. Once the model is trained, it can be used for both pairwise and groupwise registration during inference time, as described below.

3.3 Pairwise Registration

Pairwise follows straightforwardly from the training setup. Given a fixed image $\bm{x}_{f}$ and moving image $\bm{x}_{m}$ , BrainMorph performs pairwise registration as follows:

\displaystyle\begin{split}\bm{x}_{r}=\bm{x}_{m}\circ\mathcal{T}_{\theta^{*}}\ \text{where}\ \theta^{*}=\theta^{*}\left(f_{\psi}(\bm{x}_{f}),f_{\psi}(\bm{x}_{m})\right)\end{split}

(2)

Note that at test time, we can use any transformation $\mathcal{T}_{\theta}$ (e.g, rigid, affine or TPS with any hyperparameter value), which would yield a different alignment based on the same keypoints.

3.4 Groupwise Registration

Groupwise registration methods try to mitigate uncertainties associated with any one image by simultaneously registering all images in a population. This incorporates all image information in the registration process and eliminates bias towards a chosen reference frame (Toews et al., 2013b; Agier et al., 2020).

We propose a novel algorithm for groupwise registration based on detected keypoints. In the groupwise setting, we have $M$ subjects to align; thus we are solving for the optimal transformation as well as the optimal average space simultaneously. To achieve this with $N$ keypoints $\bm{P}\in\mathbb{R}^{D\times N}$ per subject, we optimize for the average space and the optimal transformations in an iterative, coordinate-ascent strategy by alternating the following two steps:

1.
Given points $\bm{P}_{k}$ at the current iteration $k$ , compute the average keypoints $\bar{\bm{P}}_{k+1}$
2.
Compute new points $\bm{P}_{k+1}$ by registering all points $\bm{P}_{k}$ to $\bar{\bm{P}}_{k+1}$

After $K$ iterations, the algorithm converges to the average space $\bar{\bm{P}}_{K}$ , and the final registration for the $i$ ’th image is found by transforming the image according to the transformation that aligns points $\bm{P}_{0}$ to $\bm{P}_{K}$ .

Note that this algorithm only relies on keypoints. Thus, it is computationally efficient since keypoints can be precomputed and done serially, whereas other works must fit all images in memory at once. In our experiments, we demonstrate the scalability of our approach by registering more than 100 volumes simultaneously.

4 Materials and Methods

4.1 Dataset

We train BrainMorph on a massive dataset of over 100,000 images from nearly 16,000 unique subjects. All datasets are gathered from publicly-available brain studies, datasets, and challenges. The full list of datasets is given in the Appendix. Our tool requires the following two widely-used pre-processing steps for all image inputs: resampling to 1mm isotropic, cropping/padding to 256x256x256. Min-max rescaling to [0, 1] is performed as the first layer in the network, and thus we do not consider it a pre-processing step.

For training, we reorient all brains to MNI space²²2During training, we apply random affine transformations as an augmentation strategy.. For purposes of obtaining training data of both non-skullstripped and skullstripped data, we perform skull-stripping on all images with HD-BET (Isensee et al., 2019), a robust deep learning-based skull-stripping tool. For images without extreme lesions, we further generate segmentations with SynthSeg (Billot et al., 2020, 2023a), which produces parcellations of 33 brain regions. We do not perform segmentation on images with extreme lesions. See the Appendix for the full list of brain regions. Datasets used for training and testing are non-overlapping, to ensure no data leakage occurs. Further details on evaluation datasets are provided in Sec. 5.1 and the Appendix.

4.2 Training Details

We are interested in learning foundational keypoints for the end goal of general-purpose brain registration. Thus, the keypoints should be optimized such that they are robust to a variety of brain MRI modalities and transformation types (rigid, affine, and nonlinear). Note that, BrainMorph is amenable to a variety of training strategies (pairwise sampling, loss function, and transformation type). We would like the network to be able to handle uni-modal, multi-modal, and longitudinal image pairs, with transform types including rigid, affine, and TPS. To do so, we perform heterogeneous training with different tasks for a single foundation model, where the task is randomly sampled in each mini-batch.

During training, we use two loss types: Dice of segmentation labels and mean-squared-error (MSE) of pixel values. We use three transformation types: rigid, affine, and TPS (nonlinear). TPS has a hyperparameter $\lambda$ which controls the degree of nonlinearity.

Table 2: Summary of BrainMorph training.

Image pair	Transform type	Loss
Normal	TPS	Dice
Skullstripped, lesion	Affine	MSE
Skullstripped, longitudinal	Rigid	MSE

In general, we are constrained by the following rules.

1.
To use MSE loss, we must sample skull-stripped same-modality pairs.
2.
For Dice loss, we may sample pairs which have corresponding segmentations (this precludes brains with lesions, for which SynthSeg (Billot et al., 2020, 2023a) cannot reliably segment).
3.
For longitudinal image pairs, we use rigid transformation to simulate realistic downstream usage.
4.
For image pairs with lesions, we use a restrictive affine transformation, as TPS will not guarantee bijective correspondence between images.

Table 2 summarizes the training strategy used, which we choose according to the above constraints. At every training iteration, we sample uniformly across the three image pair types. Thus, the model is trained to optimize the registration performance across all three image tasks with equal weighting.

We experimented with $N$ = 128, 256, and 512 keypoints, and perform a thorough analysis of the relationship between number of keypoints and registration performance in Section 6.2.2. Weights $\bm{w}$ are applied for all models during training and evaluation. For TPS transformations, we sample $\lambda$ during training from a log-uniform distribution $p(\lambda)=\text{LogUnif}(0,10)$ . During testing, we can choose a $\lambda$ value that lies in the support of this distribution. In addition, during training, in each mini-batch, we compute TPS on 32 keypoints chosen uniformly at random (Donato and Belongie, 2002). This is because TPS has a high memory requirement due to computing pairwise distances between every keypoint and grid location. Note that at test-time, we compute TPS on the full set of keypoints, and compute pairwise distances in a chunk-wise, iterative fashion to bypass this memory requirement. When minimizing Dice loss, we sample 14 regions uniformly at random for computational purposes.

For all models, we used a batch size of 1 image pair and the Adam optimizer (Kingma and Ba, 2017) for training. We train for a total of 160K gradient steps. The following uniformly-sampled augmentations were applied to the moving image across all dimensions during training: rotations $[-180\degree,+180\degree]$ , translations $[-30,30]$ voxels, scaling factor $[0.8,1.2]$ , and shear $[-0.1,0.1]$ . All training and GPU testing was performed on a machine equipped with an AMD EPYC 7513 32-Core processor and an Nvidia A100 GPU. CPU testing was performed on a machine equipped with an Intel Xeon Gold 6330 CPU @ 2.00GHz. All BrainMorph models are implemented in PyTorch.

4.3 Model Details

Table 3: BrainMorph backbone variants. Model size measured in megabytes (MB). # downsampling denotes the number of downsampling layers.

	# parameters	# downsampling	model size
BrainMorph-S	4M	4	48MB
BrainMorph-M	16M	5	196MB
BrainMorph-L	66M	6	791MB

Our architecture backbone consists of a truncated UNet, which is identical to a standard UNet except all layers which operate at the original resolution (e.g. after the last upsampling layer) are removed (Ulyanov et al., 2016). All truncated UNets we use have two convolutional blocks at each resolution. Thus, the final center-of-mass layer extracts keypoints at half-resolution. This enables us to train deeper networks with a bottleneck operating on a very coarse grid, which we empirically find leads to better performance. In particular, we report results on three variants of the truncated UNet, which differ in the capacity as a function of the number of downsampling layers. We refer to them as BrainMorph-S, BrainMorph-M, and BrainMorph-L, and summarize them in Table 3. All references to BrainMorph are BrainMorph-L models, unless otherwise noted.

4.4 Self-supervised Pretraining

We employ the following self-supervised pre-training strategy to aid in keypoint detector initialization, essentially encouraging equivariance of the keypoint extractor with respect to affine image deformations. Note that past works have leveraged equivariant networks (Billot et al., 2023b); however, we find these networks unstable to train and lack the capacity to capture variability present in our large datasets. Using a single subject, we pick a random set of keypoints $\bm{P}_{0}$ by sampling uniformly over the image coordinate grid. During pre-training, we apply random affine transformations to the input image as well as $\bm{P}_{0}$ , and minimize the following keypoint loss:

\operatorname*{arg\,min}_{\psi}\sum_{i}\mathbb{E}_{\bm{A}}\left\lVert\bm{A}\bm{P}_{0}-f_{\psi}\left(\bm{x}^{(i)}\circ\bm{A}\right)\right\rVert^{2}_{2}.

(3)

Here, $\bm{A}$ is an affine transformation drawn from a uniform distribution over the parameter space.

We train for a total of 480K gradient steps. We use the same augmentation strategy as training, except that we linearly increase the degree of augmentation such that maximum augmentation is reached after 160K gradient steps. We use the same dataset for training and pretraining. Note that we assume that all the training data are in the same orientation and roughly in the center of the image in order for the sampled keypoints to apply well to all images in the dataset.

5 Experimental Setup

5.1 Evaluation Datasets

We use the following datasets for evaluation of all models. Note that these datasets are not included in training.

1.
For healthy pairwise and cross-subject groupwise experiments, we evaluate on the IXI brain MRI dataset³³3https://brain-development.org/ixi-dataset/. Each subject has T1, T2, and PD-weighted 3D MRI scans in spatial alignment, so we can use this dataset for both unimodal and multimodal registration experiments. We evaluate on 100 subjects.
2.
For diseased subjects with lesions, we evaluate on the test split of the RSNA-ASNR-MICCAI BraTS dataset (to ensure no dataset contamination), which consists of adult brains with gliomas acquired with T1, T1gd, T2, and FLAIR sequences⁴⁴4https://www.rsna.org/rsnai/ai-image-challenge/brain-tumor-ai-challenge-2021. We also evaluate on a dataset of brains with multiple sclerosis (Muslim et al., 2022), which consists of 60 MS patients with T1, T2, and FLAIR sequences.
3.
For longitudinal experiments, we evaluate on the OASIS2 dataset, which consists of longitudinal MRI brains in nondemented and demented older adults⁵⁵5https://www.oasis-brains.org/. The number of timepoints per subject ranges between 2 and 10.

For all evaluation datasets, we perform resampling to 1mm isotropic and cropping/padding to $256^{3}$ image size, which is standard across all baselines.

We use a pre-trained and validated SynthSeg model (Billot et al., 2020) to automatically delineate 23 regions of interest (ROIs)⁶⁶6ROIs were pallidum, amygdala, caudate, cerebral cortex, hippocampus, thalamus, putamen, white matter, cerebellar cortex, ventricle, cerebral white matter, and brainstem.. Furthermore, all performance evaluations were based on examining the overlap of ROIs in the test images.

5.2 Test-time Performance Evaluation

For pairwise experiments, we use each test subject as a moving volume $\bm{x}_{m}$ , paired with another random test subject treated as a fixed volume $\bm{x}_{f}$ . We simulate different degrees of misalignment by transforming $\bm{x}_{m}$ using rotation. Rotation is applied to all 3 axes at the specified degree. We use the predicted transformation to resample the moved segmentation labels on the fixed image grid. Unimodal/multimodal registration is an independent variable in our experiments. We experiment with rigid, affine, and nonlinear registration types for all models and baselines.

For longitudinal experiments, we perform groupwise registration on all available timepoints, and restrict to rigid transformations only. For cross-subject groupwise experiments, we sample different subject, same-modality images and experiment with varying group sizes in [4, 8, 16, 32, 64, 128]. We restrict to nonlinear transformations only. Similar to pairwise experiments, we simulate different degrees of misalignment by transforming all images using rotation applied to all 3 axes at the specified degree.

5.3 Metrics

For all experiments, we quantify alignment quality and properties of the transformation using Dice overlap score and Hausdorff distance (HD).

5.4 Baselines

As the goal of this work is to develop a general-purpose tool for brain MRI registration, we wish to compare our proposed model against state-of-the-art and easily-accessible tools for this purpose. Our intended users are practitioners who desire a simple, easy-to-use tool that performs registration with minimal pre-processing or setup. Thus, we adhere to all instructions required by baselines (including intensity normalization, initial robust registration, etc.), and do not assume that data are pre-processed. Note that since skullstripping vs. non-skullstripping is an independent variable in our experiments, we do not perform any skullstripping as part of any baseline’s preprocessing requirements.

•
ITK-Elastix is a widely-used software package which supports pairwise and groupwise registration (Konstantinos Ntatsis et al., 2023). Rigid, affine, and bspline alignments are supported. For all registrations, we perform a multi-resolution pyramid strategy at 4 resolutions in order to improve the capture range and robustness of the registration. The method uses a 4D (3D+time) free-form B-spline deformation model and a similarity metric that minimizes variance of intensities under the constraint that the average deformation over images is zero. This constraint defines a true mean frame of reference that lie in the center of the population without having to calculate it explicitly.⁷⁷7https://readthedocs.org/projects/simpleelastix/downloads/pdf/latest/
•
Advanced Normalizing Tools (ANTs) is a widely-used software package which is state-of-the-art for medical image registration (Avants et al., 2009). We use the “Rigid” and “Affine” implementation for the rigid and affine model, respectively. The volumes are registered successively at three different resolutions: 0.25x, 0.5x and finally at full resolution. At 0.25x and 0.5x resolution, Gaussian smoothing with $\sigma$ of two and one voxels is applied, respectively. For non-linear registration, we use “SyN”, which performs Symmetric Normalization (Avants et al., 2008b). Finally, we used mutual information as the similarity metric for all models, which is suitable for registering images with different contrasts.
•
SynthMorph is a deep learning-based registration method which achieves agnosticism to modality/contrast by leveraging a generative strategy for synthesizing diverse images, thereby supporting multi-modal registration (Hoffmann et al., 2022). SynthMorph accepts as input the moving and fixed images and outputs a dense deformation field instead of global affine parameters, which is a common strategy in many well-performing registration models (Balakrishnan et al., 2019).
Note that an important pre-processing step required by SynthMorph is an affine-registration step to a pre-defined reference space (Reuter et al., 2010; Fischl, 2012). Thus, this limits the flexibility of SynthMorph in the sense that all registrations are performed in this reference space. In contrast, BrainMorph enables the user to define any arbitrary reference space via the fixed image. In addition, this requirement increases pre-processing time. In our experiments, we first affine register every image using ANTs (see above). SynthMorph models are implemented in Keras/Tensorflow.
•
EasyReg is a deep learning-based registration tool that supports both affine and nonlinear registration in a single pipeline (Iglesias, 2023). EasyReg is designed to be symmetric, diffeomorphic, agnostic to MRI modality and resolution (in a manner similar to SynthMorph), and does not require any preprocessing or parameter tuning.
The nonlinear registration part of EasyReg is perhaps most similar to SynthMorph, where the fixed and moving image are accepted as input to a network and the output is a dense deformation field. Unlike SynthMorph, EasyReg does not require an affine-registration step and instead performs it as an additional step in its registration pipeline. In particular, EasyReg uses a pretrained segmentation model to generate a parcellation of the brain, and keypoints are derived by computing the centroids of all 97 ROIs of the parcellation. These 97 keypoints are extracted for both the moving and fixed image, and the affine transformation is solved that aligns these keypoints corresponding to Eqn. (8). Note that this affine step crucially depends on the performance and robustness of the segmentation model.

6 Results

6.1 Main Results

6.1.1 Pairwise Registration

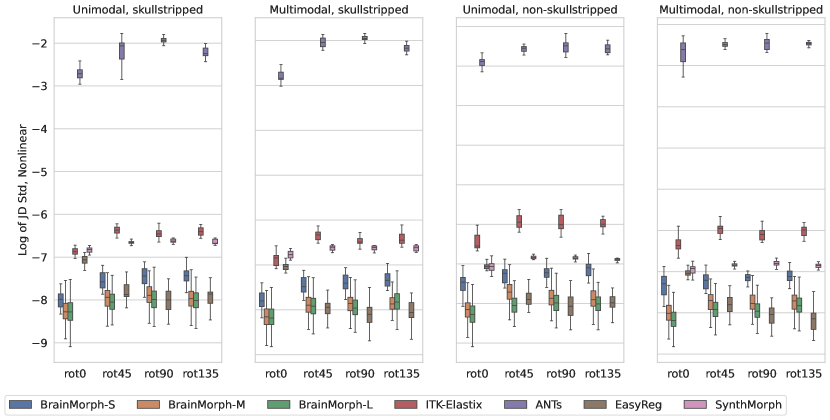
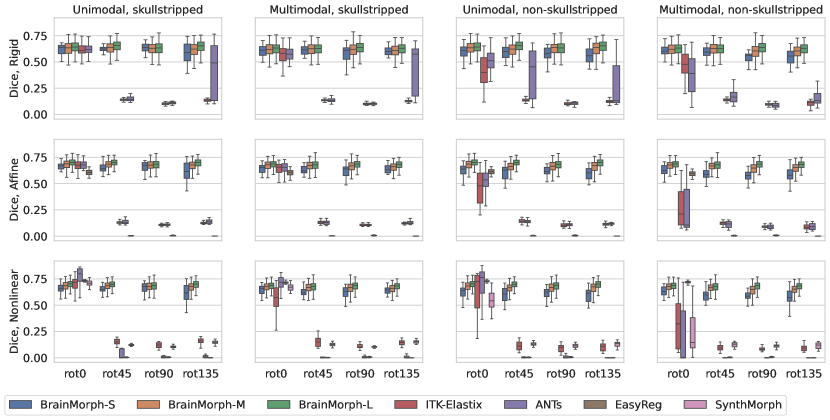
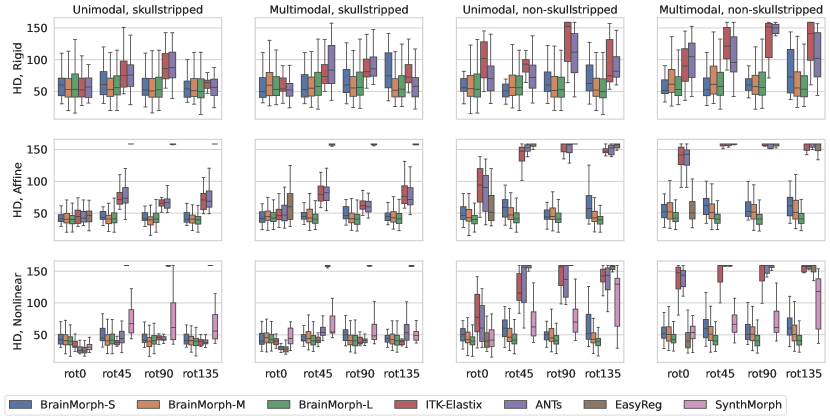
We analyze the performance of baselines and our proposed BrainMorph under conditions of large initial misalignments in terms of rotation. Figs. 3 and 4 plot overall Dice and HD across rotation angle of the moving image for baselines and BrainMorph. Each panel depicts rigid, affine, and nonlinear registrations, respectively. Each separate figure varies different combinations of unimodal vs. multimodal, skullstripped and non-skullstripped.

Generally, BrainMorph performs well across all rotation angles, modalities, and (non-)skullstripped. BrainMorph-L outperforms all baselines for rigid and affine transformations across all rotation angles. However, for the case of nonlinear unimodal and multimodal skullstripped registration at small initial misalignment (e.g. 0 degrees of rotation, (bottom left panels) ANTs, SynthMorph, and EasyReg outperform BrainMorph. We attribute this to the fact that TPS in 3D is likely not sufficient to align cortical geometry and therefore the model does not seem to identify cortical keypoints. This leads to relatively worse alignment in cortical regions, which baselines (which do not have the TPS assumption) can align better.

We find that all baseline models suffer substantially as the rotation angle increases, across all transformation types. For classical methods (ITK-Elastix and ANTs), the models fail to find correspondences when they are far apart on the spatial grid. For SynthMorph, the performance drop is likely due to not affine aligning the image pair, which is a requirement for SynthMorph but an added step in the pipeline. EasyReg accounts for this by performing an initial affine alignment, but the performance drop is due to the failure of the pretrained segmentation model (used to extract ROI centroids to be used as keypoints) to segment brains which are significantly rotated, leading to a poor initial affine alignment (see Appendix).

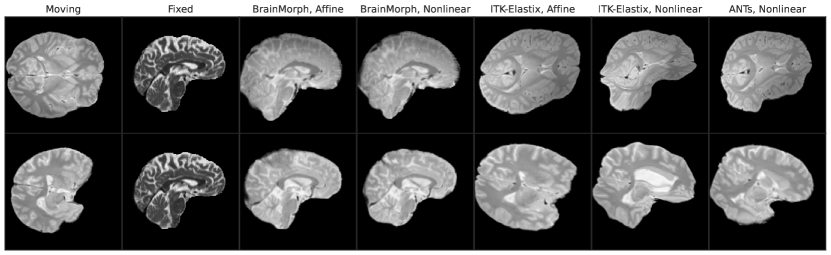
We compare the computational time across different models in Table 1. Some representative examples for all models are provided in Fig. 5 for qualitative evaluation. Overall, BrainMorph outperforms other baselines at high degrees of initial misalignment, and furthermore performs comparably or often better (at large misalignments) than the state-of-the-art ANTs registration, while requiring substantially less runtime.

6.1.2 Groupwise Registration

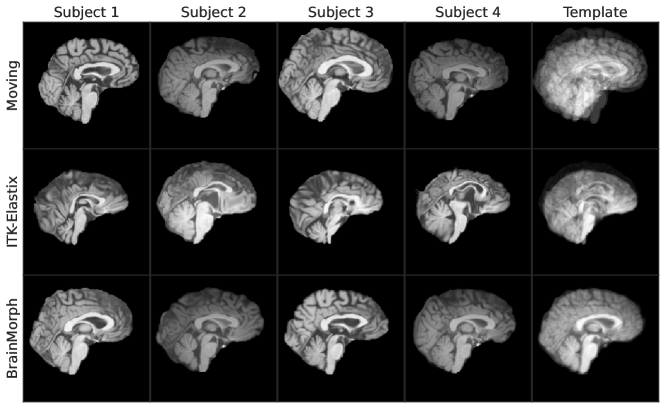
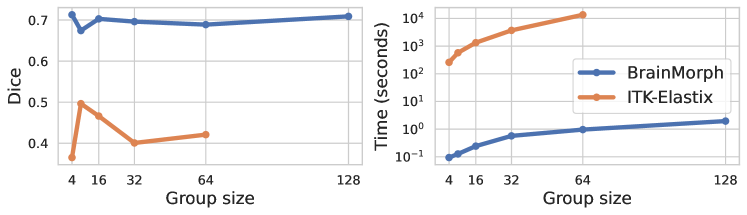
Fig. 7 depicts groupwise performance and timings for BrainMorph vs. ITK-Elastix. We use B-spline for ITK-Elastix and TPS with $\lambda=0$ for BrainMorph. We find that BrainMorph has much better and more stable performance across all group sizes we tested. Note that on our CPU, ITK-Elastix failed on 128 subjects. BrainMorph has an advantage in that keypoints can be precomputed in a serial fashion on a GPU, thus enabling much better scaling to large group sizes.

Fig. 6 depicts a representative example of groupwise registration with 4 subjects. The first row depicts the initial unaligned images, and the second and third row show the results of ITK-Elastix and BrainMorph, respectively. The last column depicts the average template brain for all 4 subjects. We find that BrainMorph groupwise registration to be substantially better, as evidenced by the sharp lines in the template brain. On a GPU, BrainMorph is also faster than ITK-Elastix by nearly 4 orders of magnitude.

6.1.3 Longitudinal Registration

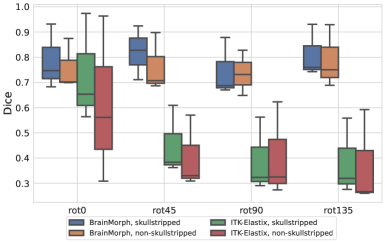
Fig 8(a) shows boxplots for longitudinal registration performance across rotation angles for skull-stripped and non-skull-stripped, respectively. We find that across all rotation angles and with and without skullstripping, BrainMorph outperforms ITK-Elastix.

6.1.4 Registration with Lesions

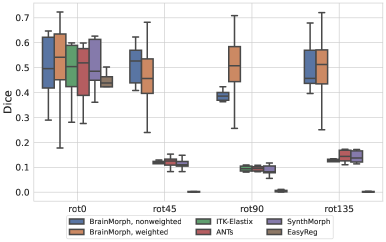
Fig 8(b) shows a boxplot of performance of all models on lesion data. We observe that the weighted variant of BrainMorph outperforms all baselines across most rotation angles and is generally has more stable performance. In particular, weighted BrainMorph tends to outperform the unweighted variant of BrainMorph at 45 degrees of rotation and above.

Note that we use Dice performance as a proxy for registration quality, even though the SynthSeg-generated segmentations are not guaranteed to be robust to diseased patients.

6.2 Keypoint Analysis

6.2.1 Visualizing keypoints

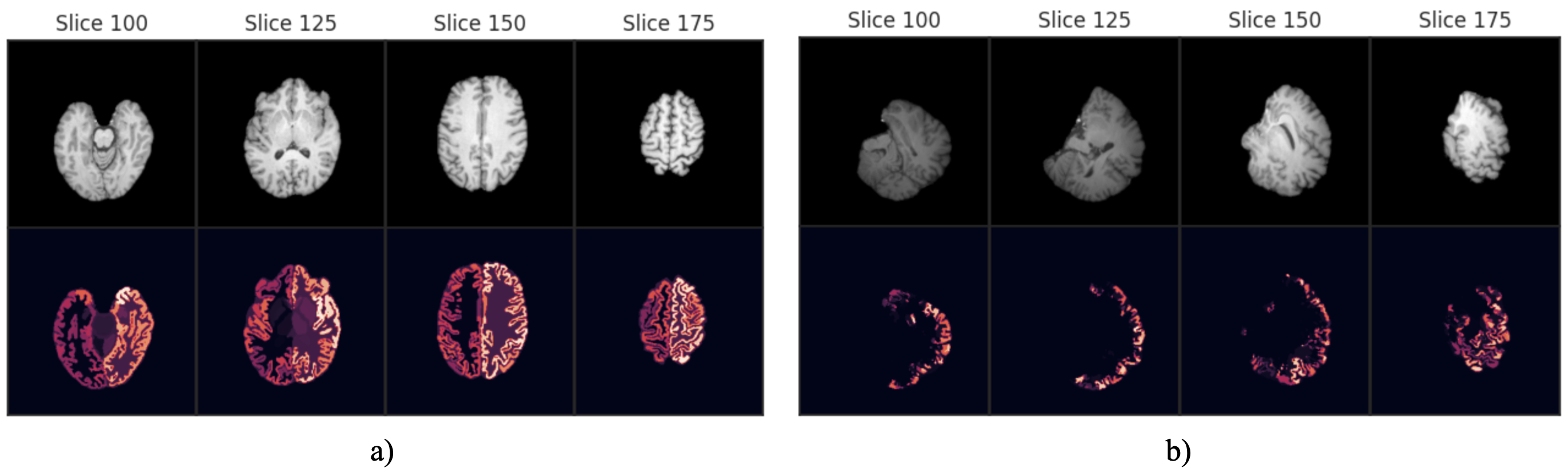
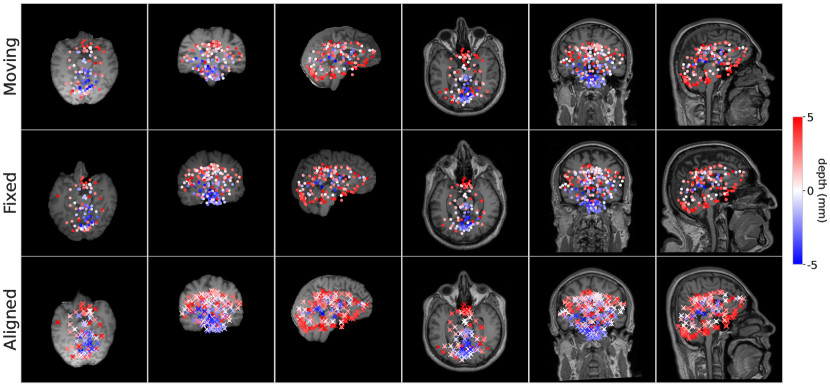
In contrast to existing models that compute the transformation parameters using a “black-box” neural network, one can investigate the keypoints that BrainMorph learns to drive the alignment. Fig. 2 shows the keypoints for a moving and fixed subject pair via mid-slices for sagittal, axial, and coronal views. The first three columns depict keypoints extracted from skull-stripped images, and the last three columns depict keypoints extracted from non-skull-stripped images. The color of the keypoints represents depth with respect to the mid-slice. The “Aligned” slices show both warped (dots) and fixed (crosses) points.

Note that keypoint locations are trained end-to-end without explicit annotations. We observe that keypoint locations are generally in sub-cortical regions, where anatomical variability is relatively low across subjects as compared to cortical regions.

6.2.2 Number of Keypoints

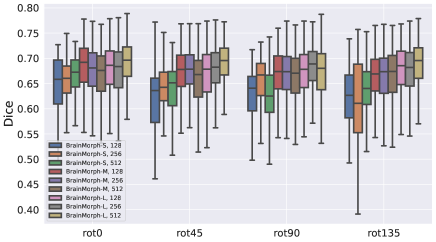
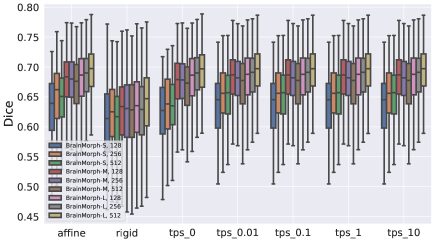
As an ablation, we examine the effect of the number of keypoints used for alignment across different transformations. We trained BrainMorph model variants with 128, 256, and 512 keypoints. Fig. 9(a) illustrates that performance is not discernably correlated to increasing the number of keypoints. We hypothesize that as keypoints are generally in subcortical regions which are anatomically stable, increasing the number of correspondences does not provide further advantage beyond a certain point. Fig. 9(b) breaks it down across different transform types, from which we can observe that performance is relatively stable across affine and different TPS transformations. We further hypothesize that due to the locations of keypoints, increasing the degree of nonlinearity doesn’t significantly lead to improved performance.

7 Discussion

The results demonstrate that BrainMorph is a robust and flexible tool for brain MRI registration. On pairwise registration, BrainMorph is generally superior to baselines across all degrees of initial misalignment, and is state-of-the-art for affine and rigid transformations. These results hold consistently for for unimodal and multimodal registration, as well as skull-stripped and non-skull-stripped data. In addition, BrainMorph does not require extensive pre-processing like skullstripping and pre-affine registration. On longitudinal and groupwise registration, BrainMorph is superior to baseline registration algorithms, while being much more memory efficient and nearly 4 orders of magnitude faster.

The main limitation of BrainMorph is nonlinear performance at low initial misalignment and skull-stripped data, for which ANTs and SynthMorph perform excellently. For this reason, users who require good nonlinear registrations may consider using BrainMorph as a robust initial alignment tool, and further performing nonlinear registration using a tool like ANTs.

8 Conclusion

We presented a robust and flexible registration tool based on the KeyMorph framework, called BrainMorph, which is a deep learning-based image registration method that uses corresponding keypoints to derive the optimal transformation that align the images. This formulation enables interpretability, robustness to large initial misalignments, and flexibility/controllability of registrations at test-time. Training on a massive dataset of over 100,000 unique images from nearly 16,000 subjects enables our tool to work on raw data with minimal pre-processing. Empirically, we demonstrate fast and competitive performance across rigid, affine, nonlinear, and groupwise registration, particularly at large degrees of initial misalignment.

Acknowledgments

We thank Benjamin Billot and Juan Eugenio Iglesias for helpful discussions. Funding for this project was in part provided by the NIH grants R01AG053949, R01AG064027 and R01AG070988, and the NSF CAREER 1748377 grant.

Ethical Standards

The work follows appropriate ethical standards in conducting research and writing the manuscript, following all applicable laws and regulations regarding treatment of animals or human subjects.

Conflicts of Interest

We declare we do not have conflicts of interest.

Data availability

All data supporting the findings of the study are publicly available. All references to data are included in the Appendix.

References

Agier et al. (2020) R. Agier, S. Valette, R. Kéchichian, L. Fanton, and R. Prost. Hubless keypoint-based 3d deformable groupwise registration. Medical Image Analysis, 59:101564, 2020. ISSN 1361-8415. . URL https://www.sciencedirect.com/science/article/pii/S1361841518306625.
Antonelli et al. (2022) Michela Antonelli, Annika Reinke, Spyridon Bakas, Keyvan Farahani, Annette Kopp-Schneider, Bennett A. Landman, Geert Litjens, Bjoern Menze, Olaf Ronneberger, Ronald M. Summers, Bram van Ginneken, Michel Bilello, Patrick Bilic, Patrick F. Christ, Richard K. G. Do, Marc J. Gollub, Stephan H. Heckers, Henkjan Huisman, William R. Jarnagin, Maureen K. McHugo, Sandy Napel, Jennifer S. Golia Pernicka, Kawal Rhode, Catalina Tobon-Gomez, Eugene Vorontsov, James A. Meakin, Sebastien Ourselin, Manuel Wiesenfarth, Pablo Arbeláez, Byeonguk Bae, Sihong Chen, Laura Daza, Jianjiang Feng, Baochun He, Fabian Isensee, Yuanfeng Ji, Fucang Jia, Ildoo Kim, Klaus Maier-Hein, Dorit Merhof, Akshay Pai, Beomhee Park, Mathias Perslev, Ramin Rezaiifar, Oliver Rippel, Ignacio Sarasua, Wei Shen, Jaemin Son, Christian Wachinger, Liansheng Wang, Yan Wang, Yingda Xia, Daguang Xu, Zhanwei Xu, Yefeng Zheng, Amber L. Simpson, Lena Maier-Hein, and M. Jorge Cardoso. The medical segmentation decathlon. Nature Communications, 13(1):4128, 2022.
Avants et al. (2008a) Brian B Avants, Charles L Epstein, Murray Grossman, and James C Gee. Symmetric diffeomorphic image registration with cross-correlation: evaluating automated labeling of elderly and neurodegenerative brain. Medical image analysis, 12(1):26–41, 2008a.
Avants et al. (2008b) Brian B Avants, Charles L Epstein, Murray Grossman, and James C Gee. Symmetric diffeomorphic image registration with cross-correlation: evaluating automated labeling of elderly and neurodegenerative brain. Medical image analysis, 12(1):26–41, 2008b.
Avants et al. (2009) Brian B Avants, Nick Tustison, and Gang Song. Advanced normalization tools (ants). Insight j, 2(365):1–35, 2009.
Balakrishnan et al. (2019) Guha Balakrishnan, Amy Zhao, Mert R. Sabuncu, John Guttag, and Adrian V. Dalca. Voxelmorph: A learning framework for deformable medical image registration. IEEE TMI, 38(8):1788–1800, Aug 2019. ISSN 1558-254X.
Barroso-Laguna et al. (2019) Axel Barroso-Laguna, Edgar Riba, Daniel Ponsa, and Krystian Mikolajczyk. Key. net: Keypoint detection by handcrafted and learned cnn filters. In Proceedings of the IEEE/CVF International Conference on Computer Vision, pages 5836–5844, 2019.
Bay et al. (2006) Herbert Bay, Tinne Tuytelaars, and Luc Van Gool. Surf: Speeded up robust features. In European conference on computer vision, pages 404–417. Springer, 2006.
Billot et al. (2020) Benjamin Billot, Douglas Greve, Koen Van Leemput, Bruce Fischl, Juan Eugenio Iglesias, and Adrian V Dalca. A learning strategy for contrast-agnostic mri segmentation. arXiv preprint arXiv:2003.01995, 2020.
Billot et al. (2023a) Benjamin Billot, Douglas N. Greve, Oula Puonti, Axel Thielscher, Koen Van Leemput, Bruce Fischl, Adrian V. Dalca, and Juan Eugenio Iglesias. Synthseg: Segmentation of brain MRI scans of any contrast and resolution without retraining. Medical Image Analysis, 86:102789, 2023a. ISSN 1361-8415.
Billot et al. (2023b) Benjamin Billot, Daniel Moyer, Neel Dey, Malte Hoffmann, Esra Abaci Turk, Borjan Gagoski, Ellen Grant, and Polina Golland. Se(3)-equivariant and noise-invariant 3d motion tracking in medical images, 2023b.
Bookstein (1989) F.L. Bookstein. Principal warps: thin-plate splines and the decomposition of deformations. IEEE Transactions on Pattern Analysis and Machine Intelligence, 11(6):567–585, 1989.
Brown et al. (2005) Matthew Brown, Richard Szeliski, and Simon Winder. Multi-image matching using multi-scale oriented patches. In 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), volume 1, pages 510–517. IEEE, 2005.
Cao et al. (2018) Xiaohuan Cao, Jianhua Yang, Jun Zhang, Qian Wang, Pew-Thian Yap, and Dinggang Shen. Deformable image registration using a cue-aware deep regression network. IEEE Transactions on Biomedical Engineering, 65(9):1900–1911, 2018.
Chen et al. (2021) Junyu Chen, Yufan He, E. Frey, Ye Li, and Yong Du. Vit-v-net: Vision transformer for unsupervised volumetric medical image registration. ArXiv, abs/2104.06468, 2021.
Chui and Rangarajan (2003) Haili Chui and Anand Rangarajan. A new point matching algorithm for non-rigid registration. Computer Vision and Image Understanding, 89(2-3):114–141, 2003.
Commowick et al. (2018) Olivier Commowick, Antoine Istace, Michael Kain, et al. Objective evaluation of multiple sclerosis lesion segmentation using a data management and processing infrastructure. Scientific Reports, 8:13650, 2018.
Dalca et al. (2019) Adrian V Dalca, Guha Balakrishnan, John Guttag, and Mert R Sabuncu. Unsupervised learning of probabilistic diffeomorphic registration for images and surfaces. Medical image analysis, 57:226–236, 2019.
de Vos et al. (2019) Bob D de Vos, Floris F Berendsen, Max A Viergever, Hessam Sokooti, Marius Staring, and Ivana Išgum. A deep learning framework for unsupervised affine and deformable image registration. Medical image analysis, 52:128–143, 2019.
DeTone et al. (2018) Daniel DeTone, Tomasz Malisiewicz, and Andrew Rabinovich. Superpoint: Self-supervised interest point detection and description. In Proceedings of the IEEE conference on computer vision and pattern recognition workshops, pages 224–236, 2018.
Donato and Belongie (2002) Gianluca Donato and Serge Belongie. Approximate thin plate spline mappings. In Anders Heyden, Gunnar Sparr, Mads Nielsen, and Peter Johansen, editors, Computer Vision — ECCV 2002, pages 21–31, Berlin, Heidelberg, 2002. Springer Berlin Heidelberg.
Dosovitskiy et al. (2015) Alexey Dosovitskiy, Philipp Fischer, Eddy Ilg, Philip Hausser, Caner Hazirbas, Vladimir Golkov, Patrick Van Der Smagt, Daniel Cremers, and Thomas Brox. Flownet: Learning optical flow with convolutional networks. In Proceedings of the IEEE international conference on computer vision, pages 2758–2766, 2015.
Eppenhof and Pluim (2018) Koen AJ Eppenhof and Josien PW Pluim. Pulmonary ct registration through supervised learning with convolutional neural networks. IEEE transactions on medical imaging, 38(5):1097–1105, 2018.
Fan et al. (2018) Jingfan Fan, Xiaohuan Cao, Zhong Xue, Pew-Thian Yap, and Dinggang Shen. Adversarial similarity network for evaluating image alignment in deep learning based registration. In International Conference on Medical Image Computing and Computer-Assisted Intervention, pages 739–746. Springer, 2018.
Fan et al. (2019) Jingfan Fan, Xiaohuan Cao, Pew-Thian Yap, and Dinggang Shen. Birnet: Brain image registration using dual-supervised fully convolutional networks. Medical image analysis, 54:193–206, 2019.
Fisch et al. (2021) Lukas Fisch, Ramona Leenings, Nils R. Winter, Udo Dannlowski, Christian Gaser, James H. Cole, and Tim Hahn. Editorial: Predicting chronological age from structural neuroimaging: The predictive analytics competition 2019. Frontiers in Psychiatry, 12, 2021. ISSN 1664-0640.
Fischl (2012) Bruce Fischl. Freesurfer. NeuroImage, 62(2):774–781, 2012.
Förstner and Gülch (1987) Wolfgang Förstner and Eberhard Gülch. A fast operator for detection and precise location of distinct points, corners and centres of circular features. In Proc. ISPRS intercommission conference on fast processing of photogrammetric data, pages 281–305. Interlaken, 1987.
Fowler et al. (2021) Christopher Fowler, Stephanie R. Rainey-Smith, Sabine Bird, J. Bomke, Pierrick Bourgeat, Belinda M. Brown, Samantha C. Burnham, Ashley I. Bush, Carly Chadunow, Steven Collins, et al. Fifteen years of the australian imaging, biomarkers and lifestyle (aibl) study: Progress and observations from 2,359 older adults spanning the spectrum from cognitive normality to alzheimer’s disease. Journal of Alzheimer’s Disease Reports, 5(1):443–468, Jun 2021. PMID: 34368630; PMCID: PMC8293663.
Frisken et al. (2020) Sarah Frisken, Ma Luo, Parikshit Juvekar, Adomas Bunevicius, Ines Machado, Prashin Unadkat, Melina M. Bertotti, Matt Toews, William M. Wells, Michael I. Miga, and Alexandra J. Golby. A comparison of thin-plate spline deformation and finite element modeling to compensate for brain shift during tumor resection. International Journal of Computer Assisted Radiology and Surgery, 15(1):75–85, 2020. . URL https://doi.org/10.1007/s11548-019-02057-2.
Gousias et al. (2012) Ioannis S. Gousias, A. David Edwards, Mary A. Rutherford, Serena J. Counsell, Joseph V. Hajnal, Daniel Rueckert, and Alexander Hammers. Magnetic resonance imaging of the newborn brain: manual segmentation of labelled atlases in term-born and preterm infants. Neuroimage, 62(3):1499–1509, Sep 2012. Epub 2012 Jun 17. PMID: 22713673.
Grøvik et al. (2020) Eirik Grøvik, Dong Yi, Michael Iv, Edward Tong, Daniel Rubin, and Greg Zaharchuk. Deep learning enables automatic detection and segmentation of brain metastases on multisequence mri. Journal of Magnetic Resonance Imaging, 51(1):175–182, Jan 2020. Epub 2019 May 2. PMID: 31050074; PMCID: PMC7199496.
Guyader et al. (2018) J. Guyader, Wyke Huizinga, D. Poot, Matthijs van Kranenburg, A. Uitterdijk, W. Niessen, and S. Klein. Groupwise image registration based on a total correlation dissimilarity measure for quantitative mri and dynamic imaging data. Scientific Reports, 8, 2018.
Harris et al. (1988) Christopher G Harris, Mike Stephens, et al. A combined corner and edge detector. In Alvey vision conference, volume 15, pages 10–5244. Citeseer, 1988.
Heinrich et al. (2012) Mattias P Heinrich, Mark Jenkinson, Manav Bhushan, Tahreema Matin, Fergus V Gleeson, Michael Brady, and Julia A Schnabel. Mind: Modality independent neighbourhood descriptor for multi-modal deformable registration. Medical image analysis, 16(7):1423–1435, 2012.
Hermosillo et al. (2002) Gerardo Hermosillo, Christophe Chefd’Hotel, and Olivier Faugeras. Variational methods for multimodal image matching. International Journal of Computer Vision, 50(3):329–343, 2002.
Hernandez Petzsche et al. (2022) M. R. Hernandez Petzsche, E. de la Rosa, U. Hanning, et al. Isles 2022: A multi-center magnetic resonance imaging stroke lesion segmentation dataset. Scientific Data, 9:762, 2022.
Hill et al. (2001) Derek LG Hill, Philipp G Batchelor, Mark Holden, and David J Hawkes. Medical image registration. Physics in medicine & biology, 46(3):R1, 2001.
Hoffmann et al. (2021) Malte Hoffmann, Benjamin Billot, Douglas N Greve, Juan Eugenio Iglesias, Bruce Fischl, and Adrian V Dalca. Synthmorph: learning contrast-invariant registration without acquired images. IEEE Transactions on Medical Imaging, 41(3):543–558, 2021.
Hoffmann et al. (2022) Malte Hoffmann, Benjamin Billot, Douglas N. Greve, Juan Eugenio Iglesias, Bruce Fischl, and Adrian V. Dalca. SynthMorph: Learning contrast-invariant registration without acquired images. IEEE Transactions on Medical Imaging, 41(3):543–558, mar 2022.
Hoopes et al. (2021) Andrew Hoopes, Malte Hoffmann, Bruce Fischl, John Guttag, and Adrian V. Dalca. Hypermorph: Amortized hyperparameter learning for image registration. IPMI, 2021.
Hu et al. (2018a) Yipeng Hu, Marc Modat, Eli Gibson, Nooshin Ghavami, Ester Bonmati, Caroline M Moore, Mark Emberton, J Alison Noble, Dean C Barratt, and Tom Vercauteren. Label-driven weakly-supervised learning for multimodal deformable image registration. In 2018 IEEE 15th International Symposium on Biomedical Imaging (ISBI 2018), pages 1070–1074. IEEE, 2018a.
Hu et al. (2018b) Yipeng Hu, Marc Modat, Eli Gibson, Wenqi Li, Nooshin Ghavami, Ester Bonmati, Guotai Wang, Steven Bandula, Caroline M Moore, Mark Emberton, et al. Weakly-supervised convolutional neural networks for multimodal image registration. Medical image analysis, 49:1–13, 2018b.
Iglesias (2023) Juan Eugenio Iglesias. A ready-to-use machine learning tool for symmetric multi-modality registration of brain mri. Scientific Reports, 13(1):6657, 2023. . URL https://doi.org/10.1038/s41598-023-33781-0.
Isensee et al. (2019) Fabian Isensee, Marianne Schell, Irada Pflueger, Gianluca Brugnara, David Bonekamp, Ulf Neuberger, Antje Wick, Heinz-Peter Schlemmer, Sabine Heiland, Wolfgang Wick, Martin Bendszus, Klaus H. Maier-Hein, and Philipp Kickingereder. Automated brain extraction of multisequence mri using artificial neural networks. Human Brain Mapping, 40(17):4952–4964, 2019.
Kazerooni et al. (2024) Anahita Fathi Kazerooni, Nastaran Khalili, Xinyang Liu, Debanjan Haldar, Zhifan Jiang, Syed Muhammed Anwar, Jake Albrecht, Maruf Adewole, Udunna Anazodo, Hannah Anderson, Sina Bagheri, Ujjwal Baid, Timothy Bergquist, Austin J. Borja, Evan Calabrese, Verena Chung, Gian-Marco Conte, Farouk Dako, James Eddy, Ivan Ezhov, Ariana Familiar, Keyvan Farahani, Shuvanjan Haldar, Juan Eugenio Iglesias, Anastasia Janas, Elaine Johansen, Blaise V Jones, Florian Kofler, Dominic LaBella, Hollie Anne Lai, Koen Van Leemput, Hongwei Bran Li, Nazanin Maleki, Aaron S McAllister, Zeke Meier, Bjoern Menze, Ahmed W Moawad, Khanak K Nandolia, Julija Pavaine, Marie Piraud, Tina Poussaint, Sanjay P Prabhu, Zachary Reitman, Andres Rodriguez, Jeffrey D Rudie, Mariana Sanchez-Montano, Ibraheem Salman Shaikh, Lubdha M. Shah, Nakul Sheth, Russel Taki Shinohara, Wenxin Tu, Karthik Viswanathan, Chunhao Wang, Jeffrey B Ware, Benedikt Wiestler, Walter Wiggins, Anna Zapaishchykova, Mariam Aboian, Miriam Bornhorst, Peter de Blank, Michelle Deutsch, Maryam Fouladi, Lindsey Hoffman, Benjamin Kann, Margot Lazow, Leonie Mikael, Ali Nabavizadeh, Roger Packer, Adam Resnick, Brian Rood, Arastoo Vossough, Spyridon Bakas, and Marius George Linguraru. The brain tumor segmentation (brats) challenge 2023: Focus on pediatrics (cbtn-connect-dipgr-asnr-miccai brats-peds), 2024.
Khan et al. (2021) Salman Hameed Khan, Muzammal Naseer, Munawar Hayat, Syed Waqas Zamir, F. Khan, and M. Shah. Transformers in vision: A survey. ACM Computing Surveys (CSUR), 54:1 – 41, 2021.
Kingma and Ba (2017) Diederik P. Kingma and Jimmy Ba. Adam: A method for stochastic optimization. arXiv preprint arXiv:1412.6980, 2017.
Konstantinos Ntatsis et al. (2023) Konstantinos Ntatsis, Niels Dekker, Viktor van der Valk, Tom Birdsong, Dženan Zukić, Stefan Klein, Marius Staring, and Matthew McCormick. itk-elastix: Medical image registration in Python. In Meghann Agarwal, Chris Calloway, and Dillon Niederhut, editors, Proceedings of the 22nd Python in Science Conference, pages 101 – 105, 2023.
Krebs et al. (2019) Julian Krebs, Hervé Delingette, Boris Mailhé, Nicholas Ayache, and Tommaso Mansi. Learning a probabilistic model for diffeomorphic registration. IEEE transactions on medical imaging, 38(9):2165–2176, 2019.
Kuijf et al. (2019) Hugo J. Kuijf, J. Matthijs Biesbroek, Jeroen De Bresser, Rutger Heinen, Simon Andermatt, Mariana Bento, Matt Berseth, Mikhail Belyaev, M. Jorge Cardoso, Adria Casamitjana, et al. Standardized assessment of automatic segmentation of white matter hyperintensities and results of the wmh segmentation challenge. IEEE Transactions on Medical Imaging, 38(11):2556–2568, Nov 2019. Epub 2019 Mar 19. PMID: 30908194; PMCID: PMC7590957.
LaMontagne et al. (2019) Pamela J. LaMontagne, Tammie LS. Benzinger, John C. Morris, Sarah Keefe, Russ Hornbeck, Chengjie Xiong, Elizabeth Grant, Jason Hassenstab, Krista Moulder, Andrei G. Vlassenko, Marcus E. Raichle, Carlos Cruchaga, and Daniel Marcus. Oasis-3: Longitudinal neuroimaging, clinical, and cognitive dataset for normal aging and alzheimer disease. medRxiv, 2019.
Lee et al. (2019a) Matthew C. H. Lee, Ozan Oktay, Andreas Schuh, Michiel Schaap, and Ben Glocker. Image-and-spatial transformer networks for structure-guided image registration, 2019a.
Lee et al. (2019b) Matthew CH Lee, Ozan Oktay, Andreas Schuh, Michiel Schaap, and Ben Glocker. Image-and-spatial transformer networks for structure-guided image registration. In International Conference on Medical Image Computing and Computer-Assisted Intervention, pages 337–345. Springer, 2019b.
Lenc and Vedaldi (2016) Karel Lenc and Andrea Vedaldi. Learning covariant feature detectors. In European conference on computer vision, pages 100–117. Springer, 2016.
Liu et al. (2021) Fengze Liu, Ke Yan, Adam Harrison, Dazhou Guo, Le Lu, Alan Yuille, Lingyun Huang, Guotong Xie, Jing Xiao, Xianghua Ye, and Dakai Jin. Same: Deformable image registration based on self-supervised anatomical embeddings, 2021.
Lowe (2004) David G Lowe. Distinctive image features from scale-invariant keypoints. International journal of computer vision, 60(2):91–110, 2004.
Ma et al. (2021) Jiayi Ma, Xingyu Jiang, Aoxiang Fan, Junjun Jiang, and Junchi Yan. Image matching from handcrafted to deep features: A survey. International Journal of Computer Vision, 129(1):23–79, 2021.
Ma et al. (2022) Mingrui Ma, Lei Song, Yuanbo Xu, and Gui-Xian Liu. Symmetric transformer-based network for unsupervised image registration. Knowl. Based Syst., 257:109959, 2022.
Ma et al. (2020) Tianyu Ma, Ajay Gupta, and Mert R Sabuncu. Volumetric landmark detection with a multi-scale shift equivariant neural network. International Symposium on Biomedical Imaging (ISBI), pages 981–985, 2020.
Machado et al. (2018) Inês Machado, Matthew Toews, Jie Luo, Prashin Unadkat, Walid Essayed, Elizabeth George, Pedro Teodoro, Herculano Carvalho, Jorge Martins, Polina Golland, Steve Pieper, Sarah Frisken, Alexandra Golby, and William Wells. Non-rigid registration of 3d ultrasound for neurosurgery using automatic feature detection and matching. International Journal of Computer Assisted Radiology and Surgery, 13(10):1525–1538, 2018. . URL https://doi.org/10.1007/s11548-018-1786-7.
Malinin et al. (2022) Andrey Malinin, Andreas Athanasopoulos, Muhamed Barakovic, Meritxell Bach Cuadra, Mark J. F. Gales, Cristina Granziera, Mara Graziani, Nikolay Kartashev, Konstantinos Kyriakopoulos, Po-Jui Lu, Nataliia Molchanova, Antonis Nikitakis, Vatsal Raina, Francesco La Rosa, Eli Sivena, Vasileios Tsarsitalidis, Efi Tsompopoulou, and Elena Volf. Shifts 2.0: Extending the dataset of real distributional shifts, 2022.
Marcus et al. (2007) Daniel S. Marcus, Tracy H. Wang, Jamie Parker, John G. Csernansky, John C. Morris, and Randy L. Buckner. Open Access Series of Imaging Studies (OASIS): Cross-sectional MRI Data in Young, Middle Aged, Nondemented, and Demented Older Adults. Journal of Cognitive Neuroscience, 19(9):1498–1507, 09 2007. ISSN 0898-929X.
Marcus et al. (2010) Daniel S. Marcus, Anthony F. Fotenos, John G. Csernansky, John C. Morris, and Randy L. Buckner. Open Access Series of Imaging Studies: Longitudinal MRI Data in Nondemented and Demented Older Adults. Journal of Cognitive Neuroscience, 22(12):2677–2684, 12 2010. ISSN 0898-929X.
Marek et al. (2011) Kenneth Marek, Danna Jennings, Shirley Lasch, Andrew Siderowf, Caroline Tanner, Tanya Simuni, Chris Coffey, Karl Kieburtz, Emily Flagg, Sohini Chowdhury, Werner Poewe, Brit Mollenhauer, Paracelsus-Elena Klinik, Todd Sherer, Mark Frasier, Claire Meunier, Alice Rudolph, Cindy Casaceli, John Seibyl, Susan Mendick, Norbert Schuff, Ying Zhang, Arthur Toga, Karen Crawford, Alison Ansbach, Pasquale De Blasio, Michele Piovella, John Trojanowski, Les Shaw, Andrew Singleton, Keith Hawkins, Jamie Eberling, Deborah Brooks, David Russell, Laura Leary, Stewart Factor, Barbara Sommerfeld, Penelope Hogarth, Emily Pighetti, Karen Williams, David Standaert, Stephanie Guthrie, Robert Hauser, Holly Delgado, Joseph Jankovic, Christine Hunter, Matthew Stern, Baochan Tran, Jim Leverenz, Marne Baca, Sam Frank, Cathi-Ann Thomas, Irene Richard, Cheryl Deeley, Linda Rees, Fabienne Sprenger, Elisabeth Lang, Holly Shill, Sanja Obradov, Hubert Fernandez, Adrienna Winters, Daniela Berg, Katharina Gauss, Douglas Galasko, Deborah Fontaine, Zoltan Mari, Melissa Gerstenhaber, David Brooks, Sophie Malloy, Paolo Barone, Katia Longo, Tom Comery, Bernard Ravina, Igor Grachev, Kim Gallagher, Michelle Collins, Katherine L. Widnell, Suzanne Ostrowizki, Paulo Fontoura, Tony Ho, Johan Luthman, Marcel van der Brug, Alastair D. Reith, and Peggy Taylor. The parkinson progression marker initiative (ppmi). Progress in Neurobiology, 95(4):629–635, 2011. ISSN 0301-0082. Biological Markers for Neurodegenerative Diseases.
Matas et al. (2004) Jiri Matas, Ondrej Chum, Martin Urban, and Tomás Pajdla. Robust wide-baseline stereo from maximally stable extremal regions. Image and vision computing, 22(10):761–767, 2004.
Mattes et al. (2003) David Mattes, David R Haynor, Hubert Vesselle, Thomas K Lewellen, and William Eubank. Pet-ct image registration in the chest using free-form deformations. IEEE transactions on medical imaging, 22(1):120–128, 2003.
Menze et al. (2015) Bjoern H. Menze, Andras Jakab, Stefan Bauer, Jayashree Kalpathy-Cramer, Keyvan Farahani, Justin Kirby, Yuliya Burren, Nicole Porz, Johannes Slotboom, Roland Wiest, Levente Lanczi, Elizabeth Gerstner, Marc-Andre Weber, Tal Arbel, Brian B. Avants, Nicholas Ayache, Patricia Buendia, D. Louis Collins, Nicolas Cordier, Jason J. Corso, Antonio Criminisi, Tilak Das, Herve Delingette, Cagatay Demiralp, Christopher R. Durst, Michel Dojat, Senan Doyle, Joana Festa, Florence Forbes, Ezequiel Geremia, Ben Glocker, Polina Golland, Xiaotao Guo, Andac Hamamci, Khan M. Iftekharuddin, Raj Jena, Nigel M. John, Ender Konukoglu, Danial Lashkari, José António Mariz, Raphael Meier, Sérgio Pereira, Doina Precup, Stephen J. Price, Tammy Riklin Raviv, Syed M. S. Reza, Michael Ryan, Duygu Sarikaya, Lawrence Schwartz, Hoo-Chang Shin, Jamie Shotton, Carlos A. Silva, Nuno Sousa, Nagesh K. Subbanna, Gabor Szekely, Thomas J. Taylor, Owen M. Thomas, Nicholas J. Tustison, Gozde Unal, Flor Vasseur, Max Wintermark, Dong Hye Ye, Liang Zhao, Binsheng Zhao, Darko Zikic, Marcel Prastawa, Mauricio Reyes, and Koen Van Leemput. The multimodal brain tumor image segmentation benchmark (brats). IEEE Transactions on Medical Imaging, 34(10):1993–2024, 2015.
Montesinos et al. (1998) Philippe Montesinos, Valérie Gouet, and Rachid Deriche. Differential invariants for color images. In Proceedings. Fourteenth International Conference on Pattern Recognition (Cat. No. 98EX170), volume 1, pages 838–840. IEEE, 1998.
Moyer et al. (2021) Daniel Moyer, Esra Abaci Turk, P Ellen Grant, William M Wells, and Polina Golland. Equivariant filters for efficient tracking in 3d imaging. In Medical Image Computing and Computer Assisted Intervention–MICCAI 2021: 24th International Conference, Strasbourg, France, September 27–October 1, 2021, Proceedings, Part IV 24, pages 193–202. Springer, 2021.
Muslim et al. (2022) A.M. Muslim, S. Mashohor, G.A. Gawwam, R. Mahmud, M.B. Hanafi, O. Alnuaimi, R. Josephine, and A.D. Almutairi. Brain mri dataset of multiple sclerosis with consensus manual lesion segmentation and patient meta information. Data Brief, 42:108139, Apr 2022.
Oliveira and Tavares (2014) Francisco PM Oliveira and Joao Manuel RS Tavares. Medical image registration: a review. Computer methods in biomechanics and biomedical engineering, 17(2):73–93, 2014.
Ono et al. (2018) Yuki Ono, Eduard Trulls, Pascal Fua, and Kwang Moo Yi. Lf-net: Learning local features from images. arXiv preprint arXiv:1805.09662, 2018.
Pérez-García et al. (2020) Fernando Pérez-García, Roman Rodionov, Ali Alim-Marvasti, Rachel Sparks, John S. Duncan, and Sébastien Ourselin. Simulation of brain resection for cavity segmentation using self-supervised and semi-supervised learning. In Anne L. Martel, Purang Abolmaesumi, Danail Stoyanov, Diana Mateus, Maria A. Zuluaga, S. Kevin Zhou, Daniel Racoceanu, and Leo Joskowicz, editors, Medical Image Computing and Computer Assisted Intervention – MICCAI 2020, pages 115–125, Cham, 2020. Springer International Publishing. ISBN 978-3-030-59716-0.
Petersen et al. (2010) Ronald C. Petersen, Paul S. Aisen, Laurel A. Beckett, Michael C. Donohue, Anthony C. Gamst, Danielle J. Harvey, Clifford R. Jr Jack, William J. Jagust, Leslie M. Shaw, Arthur W. Toga, John Q. Trojanowski, and Michael W. Weiner. Alzheimer’s disease neuroimaging initiative (adni): clinical characterization. Neurology, 74(3):201–209, Jan 2010. Epub 2009 Dec 30. PMID: 20042704; PMCID: PMC2809036.
Qin et al. (2019) Chen Qin, Bibo Shi, Rui Liao, Tommaso Mansi, Daniel Rueckert, and Ali Kamen. Unsupervised deformable registration for multi-modal images via disentangled representations. Lecture Notes in Computer Science Information Processing in Medical Imaging, page 249–261, 2019.
Reuter et al. (2010) Martin Reuter, H. Diana Rosas, and Bruce Fischl. Highly accurate inverse consistent registration: a robust approach. Neuroimage, 53(4):1181–1196, Dec 2010. Epub 2010 Jul 14. PMID: 20637289; PMCID: PMC2946852.
Rohr et al. (2001) K. Rohr, H.S. Stiehl, R. Sprengel, T.M. Buzug, J. Weese, and M.H. Kuhn. Landmark-based elastic registration using approximating thin-plate splines. IEEE Transactions on Medical Imaging, 20(6):526–534, 2001.
Rosenfeld and Thurston (1971) Azriel Rosenfeld and Mark Thurston. Edge and curve detection for visual scene analysis. IEEE Transactions on computers, 100(5):562–569, 1971.
Rudie et al. (2022) Jeffrey D. Rudie, Evan Calabrese, Rachit Saluja, David Weiss, John B. Colby, Soonmee Cha, Christopher P. Hess, Andreas M. Rauschecker, Leo P. Sugrue, and Javier E. Villanueva-Meyer. Longitudinal assessment of posttreatment diffuse glioma tissue volumes with three-dimensional convolutional neural networks. Radiology: Artificial Intelligence, 4(5):e210243, 2022.
Rudie et al. (2024) Jeffrey D. Rudie, Rachit Saluja, David A. Weiss, Pierre Nedelec, Evan Calabrese, John B. Colby, Benjamin Laguna, John Mongan, Steve Braunstein, Christopher P. Hess, Andreas M. Rauschecker, Leo P. Sugrue, and Javier E. Villanueva-Meyer. The university of california san francisco brain metastases stereotactic radiosurgery (ucsf-bmsr) mri dataset. Radiology: Artificial Intelligence, 6(2):e230126, 2024.
Sofka et al. (2017) Michal Sofka, Fausto Milletari, Jimmy Jia, and Alex Rothberg. Fully convolutional regression network for accurate detection of measurement points. In Deep learning in medical image analysis and multimodal learning for clinical decision support, pages 258–266. Springer, 2017.
Song et al. (2022) Xinrui Song, Hanqing Chao, Xuanang Xu, Hengtao Guo, Sheng Xu, Baris Turkbey, Bradford J. Wood, Thomas Sanford, Ge Wang, and Pingkun Yan. Cross-modal attention for multi-modal image registration. Medical Image Analysis, 82:102612, 2022. ISSN 1361-8415.
Sotiras et al. (2013) Aristeidis Sotiras, Christos Davatzikos, and Nikos Paragios. Deformable medical image registration: A survey. IEEE Transactions on Medical Imaging, 32(7):1153–1190, 2013.
Tang et al. (2023) Canhui Tang, Yiheng Li, S. Du, Guofa Wang, and Zhiqiang Tian. Hd2reg: Hierarchical descriptors and detectors for point cloud registration. 2023 IEEE Intelligent Vehicles Symposium (IV), pages 1–6, 2023.
Tang et al. (2019) Jiexiong Tang, Hanme Kim, V. Guizilini, Sudeep Pillai, and Rares Ambrus. Neural outlier rejection for self-supervised keypoint learning. ArXiv, abs/1912.10615, 2019.
Toews et al. (2013a) Matthew Toews, Lilla Zöllei, and William M Wells. Feature-based alignment of volumetric multi-modal images. In International Conference on Information Processing in Medical Imaging, pages 25–36. Springer, 2013a.
Toews et al. (2013b) Matthew Toews, Lilla Zöllei, and William M. Wells. Feature-based alignment of volumetric multi-modal images. In James C. Gee, Sarang Joshi, Kilian M. Pohl, William M. Wells, and Lilla Zöllei, editors, Information Processing in Medical Imaging, pages 25–36, Berlin, Heidelberg, 2013b. Springer Berlin Heidelberg. ISBN 978-3-642-38868-2.
Tuytelaars and Mikolajczyk (2008) Tinne Tuytelaars and Krystian Mikolajczyk. Local invariant feature detectors: a survey. Now Publishers Inc, 2008.
Uludağ and Roebroeck (2014) Kâmil Uludağ and Alard Roebroeck. General overview on the merits of multimodal neuroimaging data fusion. Neuroimage, 102:3–10, 2014.
Ulyanov et al. (2016) Dmitry Ulyanov, Andrea Vedaldi, and Victor Lempitsky. Instance normalization: The missing ingredient for fast stylization. arXiv preprint arXiv:1607.08022, 2016.
Uzunova et al. (2017) Hristina Uzunova, Matthias Wilms, Heinz Handels, and Jan Ehrhardt. Training cnns for image registration from few samples with model-based data augmentation. In International Conference on Medical Image Computing and Computer-Assisted Intervention, pages 223–231. Springer, 2017.
Van de Weijer et al. (2005) Joost Van de Weijer, Theo Gevers, and Andrew D Bagdanov. Boosting color saliency in image feature detection. IEEE transactions on pattern analysis and machine intelligence, 28(1):150–156, 2005.
Verdie et al. (2015) Yannick Verdie, Kwang Yi, Pascal Fua, and Vincent Lepetit. Tilde: A temporally invariant learned detector. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 5279–5288, 2015.
Viklands (2006) T. Viklands. Algorithms for the weighted orthogonal procrustes problem and other least squares problems, 2006.
Viola and Wells III (1997) Paul Viola and William M Wells III. Alignment by maximization of mutual information. International journal of computer vision, 24(2):137–154, 1997.
Wachinger et al. (2018) Christian Wachinger, Matthew Toews, Georg Langs, William Wells, and Polina Golland. Keypoint transfer for fast whole-body segmentation. IEEE transactions on medical imaging, 39(2):273–282, 2018.
Wang et al. (2023) Alan Q. Wang, Evan M. Yu, Adrian V. Dalca, and Mert R. Sabuncu. A robust and interpretable deep learning framework for multi-modal registration via keypoints. Medical Image Analysis, 90:102962, 2023. ISSN 1361-8415.
Wu et al. (2015) Guorong Wu, Minjeong Kim, Qian Wang, Brent C Munsell, and Dinggang Shen. Scalable high-performance image registration framework by unsupervised deep feature representations learning. IEEE Transactions on Biomedical Engineering, 63(7):1505–1516, 2015.
Yang et al. (2017) Xiao Yang, Roland Kwitt, Martin Styner, and Marc Niethammer. Quicksilver: Fast predictive image registration–a deep learning approach. NeuroImage, 158:378–396, 2017.
Yi et al. (2016) Kwang Moo Yi, Eduard Trulls, Vincent Lepetit, and Pascal Fua. Lift: Learned invariant feature transform. In European conference on computer vision, pages 467–483. Springer, 2016.
Yi et al. (2018) Kwang Moo Yi, Eduard Trulls, Yuki Ono, Vincent Lepetit, Mathieu Salzmann, and Pascal Fua. Learning to find good correspondences, 2018.
Yu et al. (2022) Evan M Yu, Alan Q. Wang, Adrian V Dalca, and Mert R. Sabuncu. Keymorph: Robust multi-modal affine registration via unsupervised keypoint detection. In Medical Imaging with Deep Learning, 2022.
Zhang et al. (2022) Junkang Zhang, Yiqian Wang, Ji Dai, Melina Cavichini, Dirk-Uwe G. Bartsch, William R. Freeman, Truong Q. Nguyen, and Cheolhong An. Two-step registration on multi-modal retinal images via deep neural networks. IEEE Transactions on Image Processing, 31:823–838, 2022.

A Details on the Keypoint Detection Network

The keypoint detector in BrainMorph is a UNet-style architecture, but that is truncated at the last upsampling layer. Thus, keypoints are extracted at half resolution; this is done for balancing quality of extracted keypoints with computational feasibility.

The UNet is composed of $d$ number of levels (i.e. downsampling layers), with 2 convolutional blocks per level. $d=\{4,5,6\}$ corresponds to BrainMorph-{S, M, L}, respectively. Each level has its corresponding block in the upsampling part of the UNet, except for the final resolution. Each convolutional block consists of a convolutional layer, an instance normalization, and a ReLU nonlinearity. The number of channels starts at 32 and doubles with every level.

B Differentiable, Closed-Form Coordinate Transformations

Notation: In the following sections, column vectors are lower-case bolded and matrices are upper-case bolded. $D$ -dimensional coordinates are represented as column vectors, i.e. $\bm{p}\in\mathbb{R}^{D}$ . $D$ is typically 2 or 3. $\tilde{\bm{p}}$ denotes $\bm{p}$ in homogeneous coordinates, i.e. $\tilde{\bm{p}}=[\bm{p},1]^{T}$ . Superscripts in parentheses $\bm{p}^{(i)}$ index over separate instances of $\bm{p}$ (e.g. in a dataset), whereas subscripts $\bm{p}_{i}$ denotes the $i$ ’th element of $\bm{p}$ .

We summarize three parametric transformation families that can be derived in closed-form, from corresponding keypoint pairs. Suppose we have a set of $N$ corresponding keypoint pairs $\{(\bm{p}^{(i)},\bm{q}^{(i)})\}_{i=1}^{N}$ , where $\bm{p}^{(i)},\bm{q}^{(i)}\in\mathbb{R}^{D}$ and $N>D$ . For convenience, let $\bm{P}:=\begin{bmatrix}\bm{p}^{(1)}&...&\bm{p}^{(N)}\end{bmatrix}\in\mathbb{R}^{D\times N}$ , and similarly for $\tilde{\bm{P}}$ and $\bm{Q}$ . Define $\mathcal{T}_{\theta}:\mathbb{R}^{D}\rightarrow\mathbb{R}^{D}$ as a family of coordinate transformations, where $\theta\in\Theta$ are parameters of the transformation. For all transformation families, we also consider weighted versions, where we have weights for each correspondence $\{w_{i}\}_{i=1}^{N}$ . For convenience, let $\bm{W}=\text{diag}(w_{1},...,w_{N})$ .

B.1 Rigid

Rigid transformations apply a rotation $\bm{R}\in\mathbb{R}^{D\times D}$ and a translation $\bm{t}\in\mathbb{R}^{D\times 1}$ to a coordinate:

\mathcal{T}_{\theta}(\bm{p})=\bm{R}\bm{p}+\bm{t},

(4)

where the parameter set is the elements of the matrix and vector, $\theta=\{\bm{R},\bm{t}\}$ .

The optimal translation is estimated by subtracting the weighted centroids of the moving and fixed point clouds:

\bm{t}^{*}=\bar{\bm{p}}-\bar{\bm{q}},

(5)

where $\bar{\bm{p}}=\sum_{i}\bm{p}^{(i)}$ for non-weighted and $\bar{\bm{p}}=\sum_{i}w_{i}\bm{p}^{(i)}$ for weighted, and similarly for $\bar{\bm{q}}$ .

The optimal rotation is well-studied and is known as the orthogonal Procrustes problem (Viklands, 2006). First, denote by $\bar{\bm{P}}$ the centered version of $\bm{P}$ where each column is subtracted by the centroid $\bar{\bm{p}}$ , and similarly for $\bar{\bm{Q}}$ . Next, compute the SVD of the weighted cross-correlation matrix $\text{SVD}(\bm{\Sigma})=\text{SVD}(\bar{\bm{P}}^{T}\bar{\bm{Q}})=\bm{U}\bm{\Lambda}\bm{V}^{T}$ . For weighted, $\Sigma=\bar{\bm{P}}^{T}\bm{W}\bar{\bm{Q}}$ . Then, $\bm{R}^{*}=\bm{V}\bm{U}^{T}$ .

B.2 Affine

Affine transformations are represented as a matrix multiplication of $\bm{A}\in\mathbb{R}^{D\times(D+1)}$ with a coordinate in homogeneous form:

\mathcal{T}_{\theta}(\bm{p})=\bm{A}\tilde{\bm{p}},

(6)

where the parameter set is the elements of the matrix, $\theta=\{\bm{A}\}$ .

Given $N$ corresponding keypoint pairs, there exists a differentiable, closed-form expression for an affine transformation that aligns the keypoints:

	$\displaystyle\theta^{*}(\bm{P},\bm{Q})$	$\displaystyle:=\operatorname*{arg\,min}_{\theta}\sum_{i=1}^{N}\left(\bm{A}\tilde{\bm{p}}^{(i)}-\bm{q}^{(i)}\right)^{2}$		(7)
		$\displaystyle=\bm{Q}\tilde{\bm{P}}^{T}(\tilde{\bm{P}}\tilde{\bm{P}}^{T})^{-1}.$		(8)

To derive this solution, rewrite the objective in matrix form:

	$\displaystyle\mathcal{L}$	$\displaystyle=\sum_{i=1}^{N}\left(\bm{A}\tilde{\bm{p}}^{(i)}-\bm{q}^{(i)}\right)^{2}$
		$\displaystyle=\left\\|\bm{A}\tilde{\bm{P}}-\bm{Q}\right\\|_{F},$

where $\left\lVert\cdot\right\rVert_{F}$ denotes the Frobenius norm. Taking the derivative with respect to $\bm{A}$ and setting the result to zero, we obtain:

	$\displaystyle\frac{\partial\mathcal{L}}{\partial\bm{A}}$	$\displaystyle=(\bm{A}\tilde{\bm{P}}-\bm{Q})\tilde{\bm{P}}^{T}=\bm{0}$
		$\displaystyle\implies\bm{A}\tilde{\bm{P}}\tilde{\bm{P}}^{T}=\bm{Q}\tilde{\bm{P}}^{T}$
		$\displaystyle\implies\bm{A}=\bm{Q}\tilde{\bm{P}}^{T}(\tilde{\bm{P}}\tilde{\bm{P}}^{T})^{-1}.$

The extension to incorporate weightings for the correspondences is straightforward:

	$\displaystyle\theta^{*}(\bm{P},\bm{Q},\bm{W})$	$\displaystyle:=\operatorname*{arg\,min}_{\theta}\sum_{i=1}^{N}w_{i}\left(\bm{A}\tilde{\bm{p}}^{(i)}-\bm{q}^{(i)}\right)^{2}$		(9)
		$\displaystyle=\bm{Q}\bm{W}\tilde{\bm{P}}^{T}(\tilde{\bm{P}}\bm{W}\tilde{\bm{P}}^{T})^{-1}.$		(10)

Note that solving for the affine transformation is the least-squares solution to an overdetermined system, and thus in practice the points will not be exactly matched due to the restrictive nature of the affine transformation. This restrictiveness may be alleviated or removed by choosing a transformation family with additional degrees of freedom, as we detail next.

B.3 Thin-Plate Spline

The application of the thin-plate spline (TPS) interpolant to modeling coordinate transformations yields a parametric, non-rigid deformation model which admits a closed-form expression for the solution that interpolates a set of corresponding keypoints (Bookstein, 1989; Donato and Belongie, 2002; Rohr et al., 2001; Machado et al., 2018; Frisken et al., 2020). This provides additional degrees of freedom over the affine family of transformations, while also subsuming it as a special case.

For the $d$ ’th dimension, the TPS interpolant $\mathcal{T}_{\theta_{d}}:\mathbb{R}^{D}\rightarrow\mathbb{R}$ takes the following form:

\mathcal{T}_{\theta_{d}}(\bm{p})=(\bm{a}_{d})^{T}\tilde{\bm{p}}+\sum_{i=1}^{N}v_{i,d}U\left(\left\lVert\bm{p}^{(i)}-\bm{p}\right\rVert_{2}\right),

(11)

where $\bm{a}_{d}\in\mathbb{R}^{D+1}$ and $\{v_{i,d}\}$ constitute the transformation parameters $\theta_{d}$ and $U(r)=r^{2}\ln(r)$ . We define $\bm{A}\in\mathbb{R}^{(D+1)\times D}$ and $\bm{V}\in\mathbb{R}^{N\times D}$ as the collection of all the parameters for $d=1,...,D$ . Then, the parameter set is $\theta=\{\bm{A},\bm{V}\}$ .

This form of $\mathcal{T}$ minimizes the bending energy:

I_{\mathcal{T}}=\int_{\mathbb{R}^{D}}\left\lVert\nabla^{2}\mathcal{T}\right\rVert_{F}^{2}d\bm{p}_{1}...d\bm{p}_{D},

(12)

where $\left\lVert\cdot\right\rVert_{F}$ is the Frobenius norm and $\nabla^{2}\mathcal{T}$ is the matrix of second-order partial derivatives of $\mathcal{T}$ . For each $\theta_{d}$ , we impose interpolation conditions $\mathcal{T}_{\theta_{d}}(\bm{p}^{(i)})=\bm{q}_{d}^{(i)}$ and enforce $\mathcal{T}$ to have square-integrable second derivatives:

\sum_{i=1}^{N}v_{i,d}=0\ \ \text{and}\ \ \sum_{i=1}^{N}v_{i,d}\bm{p}_{d}=0\ \ \forall d\in\{1,...,D\}.

(13)

Given these conditions, the following system of linear equations solves for $\theta$ :

\bm{\Psi}\theta:=\begin{bmatrix}\bm{K}&\bm{L}\\ \bm{L}^{T}&\bm{O}\end{bmatrix}\begin{bmatrix}\bm{V}\\ \bm{A}\end{bmatrix}=\begin{bmatrix}\bm{Q}^{T}\\ \bm{O}\end{bmatrix}:=\bm{Z}.

(14)

Here, $\bm{K}\in\mathbb{R}^{N\times N}$ where $\bm{K}_{ij}=U\left(\left\lVert\bm{p}^{(i)}-\bm{p}^{(j)}\right\rVert_{2}\right)$ , $\bm{L}\in\mathbb{R}^{N\times(D+1)}$ where the $i$ ’th row is $(\tilde{\bm{p}}^{(i)})^{T}$ , and $\bm{O}$ is a matrix of zeros with appropriate dimensions. Thus,

\theta^{*}(\bm{P},\bm{Q}):=\bm{\Psi}^{-1}\bm{Z}.

(15)

Solving for $\theta^{*}$ is a differentiable operation.

The interpolation conditions can be relaxed (e.g. under the presence of noise) by introducing a regularization term:

\operatorname*{arg\,min}_{\theta_{d}}\sum_{i=1}^{N}\left(\mathcal{T}_{\theta_{d}}\left(\bm{p}^{(i)}\right)-\bm{q}_{d}^{(i)}\right)^{2}+\lambda I_{\mathcal{T}}

(16)

where $\lambda>0$ is a hyperparameter that controls the strength of regularization. As $\lambda$ approaches $\infty$ , the optimal $\mathcal{T}$ approaches the affine case (i.e. zero bending energy). This formulation can be solved exactly by replacing $\bm{K}$ with $\bm{K}+\lambda\bm{I}$ in Eq. (14). Importantly, $\theta$ and the optimal $\theta^{*}(\bm{P},\bm{Q})$ exhibits a dependence on $\lambda$ . Finally, weights can be incorporated by replacing $\bm{K}$ with $\bm{K}+\lambda\bm{W}^{-1}$ (Rohr et al., 2001).

C List of Datasets

A full list of datasets used for training and evaluation is shown in Table 4.

Dataset	Description	Train/Eval	No. Subjects	No. Modalities	Modalities Info	No. Images	Longitudinal?	Lesion?
BraTS-SSA-2023	African Gliloms	Train	60	4	T1 T1gd T2 FLAIR	240	✗	✓
BraTS-MEN-2023	Meningiomas	Train	1000	4	T1 T1gd T2 FLAIR	4000	✗	✓
BraTS-MET-2023	Metastases	Train	165	4	T1 T1gd T2 FLAIR	660	✗	✓
BraTS-MET-NYU-2023	Metastases	Train	164	4	T1 T1gd T2 FLAIR	656	✗	✓
BraTS-PED-2023	Pediatric Glioblastomas	Train	99	4	T1 T1gd T2 FLAIR	396	✗	✓
BraTS-MET-UCSF-2023	Metastases	Train	324	4	T1 T1gd T2 FLAIR	1296	✗	✓
BraTS-2016	Tumor	Train	1104	1	T1	1104	✗	✓
UCSF-BMSR	Metastases	Train	459	4	FLAIR T1post T1pre subtraction	1836	✗	✓
MSSEG2	Multiple Sclerosis	Train	40	1	FLAIR	80	✓	✓
Shifts-challenge-part1MSSEG	Multiple Sclerosis	Train	15	5	FLAIR T1 T2 GADO DP	75	✗	✓
Shifts-challenge-part2Ljubljana	Multiple Sclerosis	Train	25	4	FLAIR T1 T2 T1ce	100	✗	✓
Shifts-challenge-part2Best	Multiple Sclerosis	Train	21	4	FLAIR T1 T2 PD	84	✗	✓
Brain Development	Adult and Neonatal Brain Atlases	Train	33	1	T1	33	✗	✗
EPISURG	Epileptic	Train	133	1	T1	133	✗	✗
WMH	White Matter Hyperintensity	Train	120	1	T1	120	✗	✗
ISLES-2022	Ischemic Stroke Lesion	Train	250	2	DWI ADC	500	✗	✓
MedicalDecathlon-BrainTumour	Tumor	Train	484	4	FLAIR T1 T1gd T2	1936	✗	✓
UCSF-ALPTDG	Post Treatment Gliomas	Train	298	5	FLAIR T1 T1ce T2 T1csub	1490	✓	✓
StanfordMETShare	Metastases	Train	105	4	T1 FLAIR T1gd T1pre	420	✗	✓
PPMI	Parkinson’s Disease	Train	1382	1	T1	1382	✓	✗
ADNI	Alzheimer’s Disease	Train	2027	3	T1 T2 FLAIR	18645	✓	✗
PAC 2019	Normal Aging	Train	2640	1	T1	2640	✗	✗
AIBL	Alzheimer’s Disease	Train	708	1	T1	708	✗	✗
OASIS1	Normal Aging and Dementia	Train	348	1	T1	1350	✓	✗
OASIS3	Normal Aging and Alzheimer’s Disease	Train	2270	6	T1 T2 T2star FLASH FLAIR angio	10299	✓	✗
IXI	Normal	Eval	151	3	T1 T2 PD	453	✗	✗
OASIS2	Dementia	Eval	298	1	T1	1095	✓	✗
BraTS-GLI-2023 (test)	Glioblastomas	Eval	876	4	T1 T1gd T2 FLAIR	3504	✗	✓
MS-60	Multiple sclerosis	Eval	60	3	T1 T2 FLAIR	180	✗	✓
Total			15659	13 (unique)		55415 ( $\times$ 2)

Table 4: Dataset details. Total images is 55415 (possibly non-unique due to overlap).

\times

2 = 110836 to include with and without skullstripping. All citations in top-bottom row order: (Kazerooni et al., 2024), (Kazerooni et al., 2024), (Kazerooni et al., 2024), (Kazerooni et al., 2024), (Kazerooni et al., 2024), (Rudie et al., 2024), (Menze et al., 2015), (Rudie et al., 2024), (Commowick et al., 2018), (Malinin et al., 2022), (Rudie et al., 2024), (Rudie et al., 2024), (Gousias et al., 2012), (Pérez-García et al., 2020), (Kuijf et al., 2019), (Hernandez Petzsche et al., 2022), (Antonelli et al., 2022), (Rudie et al., 2022), (Grøvik et al., 2020), (Marek et al., 2011), (Petersen et al., 2010), (Fowler et al., 2021), (Fisch et al., 2021), (Marcus et al., 2007), (LaMontagne et al., 2019), https://brain-development.org/ixi-dataset/, (Marcus et al., 2010), (Kazerooni et al., 2024), (Muslim et al., 2022).

D Failure Cases of Baselines

We find that all baseline models suffer substantially as the rotation angle increases, across all transformation types. For classical methods (ITK-Elastix and ANTs), the models fail to find correspondences when they are far apart on the spatial grid. For SynthMorph, the performance drop is likely due to not affine aligning the image pair, which is a requirement for SynthMorph but an added step in the pipeline. EasyReg accounts for this by performing an initial affine alignment, but the performance drop is due to the failure of the pretrained segmentation model (used to extract ROI centroids to be used as keypoints) to segment brains which are significantly rotated, leading to a poor initial affine alignment. We visualize this in Fig. 10.

[bib.bib1] Agier et al. (2020) R. Agier, S. Valette, R. Kéchichian, L. Fanton, and R. Prost. Hubless keypoint-based 3d deformable groupwise registration. Medical Image Analysis, 59:101564, 2020. ISSN 1361-8415. . URL https://www.sciencedirect.com/science/article/pii/S1361841518306625.

[bib.bib2] Antonelli et al. (2022) Michela Antonelli, Annika Reinke, Spyridon Bakas, Keyvan Farahani, Annette Kopp-Schneider, Bennett A. Landman, Geert Litjens, Bjoern Menze, Olaf Ronneberger, Ronald M. Summers, Bram van Ginneken, Michel Bilello, Patrick Bilic, Patrick F. Christ, Richard K. G. Do, Marc J. Gollub, Stephan H. Heckers, Henkjan Huisman, William R. Jarnagin, Maureen K. McHugo, Sandy Napel, Jennifer S. Golia Pernicka, Kawal Rhode, Catalina Tobon-Gomez, Eugene Vorontsov, James A. Meakin, Sebastien Ourselin, Manuel Wiesenfarth, Pablo Arbeláez, Byeonguk Bae, Sihong Chen, Laura Daza, Jianjiang Feng, Baochun He, Fabian Isensee, Yuanfeng Ji, Fucang Jia, Ildoo Kim, Klaus Maier-Hein, Dorit Merhof, Akshay Pai, Beomhee Park, Mathias Perslev, Ramin Rezaiifar, Oliver Rippel, Ignacio Sarasua, Wei Shen, Jaemin Son, Christian Wachinger, Liansheng Wang, Yan Wang, Yingda Xia, Daguang Xu, Zhanwei Xu, Yefeng Zheng, Amber L. Simpson, Lena Maier-Hein, and M. Jorge Cardoso. The medical segmentation decathlon. Nature Communications, 13(1):4128, 2022.

[bib.bib3] Avants et al. (2008a) Brian B Avants, Charles L Epstein, Murray Grossman, and James C Gee. Symmetric diffeomorphic image registration with cross-correlation: evaluating automated labeling of elderly and neurodegenerative brain. Medical image analysis, 12(1):26–41, 2008a.

[bib.bib4] Avants et al. (2008b) Brian B Avants, Charles L Epstein, Murray Grossman, and James C Gee. Symmetric diffeomorphic image registration with cross-correlation: evaluating automated labeling of elderly and neurodegenerative brain. Medical image analysis, 12(1):26–41, 2008b.

[bib.bib5] Avants et al. (2009) Brian B Avants, Nick Tustison, and Gang Song. Advanced normalization tools (ants). Insight j, 2(365):1–35, 2009.

[bib.bib6] Balakrishnan et al. (2019) Guha Balakrishnan, Amy Zhao, Mert R. Sabuncu, John Guttag, and Adrian V. Dalca. Voxelmorph: A learning framework for deformable medical image registration. IEEE TMI, 38(8):1788–1800, Aug 2019. ISSN 1558-254X.

[bib.bib7] Barroso-Laguna et al. (2019) Axel Barroso-Laguna, Edgar Riba, Daniel Ponsa, and Krystian Mikolajczyk. Key. net: Keypoint detection by handcrafted and learned cnn filters. In Proceedings of the IEEE/CVF International Conference on Computer Vision, pages 5836–5844, 2019.

[bib.bib8] Bay et al. (2006) Herbert Bay, Tinne Tuytelaars, and Luc Van Gool. Surf: Speeded up robust features. In European conference on computer vision, pages 404–417. Springer, 2006.

[bib.bib9] Billot et al. (2020) Benjamin Billot, Douglas Greve, Koen Van Leemput, Bruce Fischl, Juan Eugenio Iglesias, and Adrian V Dalca. A learning strategy for contrast-agnostic mri segmentation. arXiv preprint arXiv:2003.01995, 2020.

[bib.bib10] Billot et al. (2023a) Benjamin Billot, Douglas N. Greve, Oula Puonti, Axel Thielscher, Koen Van Leemput, Bruce Fischl, Adrian V. Dalca, and Juan Eugenio Iglesias. Synthseg: Segmentation of brain MRI scans of any contrast and resolution without retraining. Medical Image Analysis, 86:102789, 2023a. ISSN 1361-8415.

[bib.bib11] Billot et al. (2023b) Benjamin Billot, Daniel Moyer, Neel Dey, Malte Hoffmann, Esra Abaci Turk, Borjan Gagoski, Ellen Grant, and Polina Golland. Se(3)-equivariant and noise-invariant 3d motion tracking in medical images, 2023b.

[bib.bib12] Bookstein (1989) F.L. Bookstein. Principal warps: thin-plate splines and the decomposition of deformations. IEEE Transactions on Pattern Analysis and Machine Intelligence, 11(6):567–585, 1989.

[bib.bib13] Brown et al. (2005) Matthew Brown, Richard Szeliski, and Simon Winder. Multi-image matching using multi-scale oriented patches. In 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), volume 1, pages 510–517. IEEE, 2005.

[bib.bib14] Cao et al. (2018) Xiaohuan Cao, Jianhua Yang, Jun Zhang, Qian Wang, Pew-Thian Yap, and Dinggang Shen. Deformable image registration using a cue-aware deep regression network. IEEE Transactions on Biomedical Engineering, 65(9):1900–1911, 2018.

[bib.bib15] Chen et al. (2021) Junyu Chen, Yufan He, E. Frey, Ye Li, and Yong Du. Vit-v-net: Vision transformer for unsupervised volumetric medical image registration. ArXiv, abs/2104.06468, 2021.

[bib.bib16] Chui and Rangarajan (2003) Haili Chui and Anand Rangarajan. A new point matching algorithm for non-rigid registration. Computer Vision and Image Understanding, 89(2-3):114–141, 2003.

[bib.bib17] Commowick et al. (2018) Olivier Commowick, Antoine Istace, Michael Kain, et al. Objective evaluation of multiple sclerosis lesion segmentation using a data management and processing infrastructure. Scientific Reports, 8:13650, 2018.

[bib.bib18] Dalca et al. (2019) Adrian V Dalca, Guha Balakrishnan, John Guttag, and Mert R Sabuncu. Unsupervised learning of probabilistic diffeomorphic registration for images and surfaces. Medical image analysis, 57:226–236, 2019.

[bib.bib19] de Vos et al. (2019) Bob D de Vos, Floris F Berendsen, Max A Viergever, Hessam Sokooti, Marius Staring, and Ivana Išgum. A deep learning framework for unsupervised affine and deformable image registration. Medical image analysis, 52:128–143, 2019.

[bib.bib20] DeTone et al. (2018) Daniel DeTone, Tomasz Malisiewicz, and Andrew Rabinovich. Superpoint: Self-supervised interest point detection and description. In Proceedings of the IEEE conference on computer vision and pattern recognition workshops, pages 224–236, 2018.

[bib.bib21] Donato and Belongie (2002) Gianluca Donato and Serge Belongie. Approximate thin plate spline mappings. In Anders Heyden, Gunnar Sparr, Mads Nielsen, and Peter Johansen, editors, Computer Vision — ECCV 2002, pages 21–31, Berlin, Heidelberg, 2002. Springer Berlin Heidelberg.

[bib.bib22] Dosovitskiy et al. (2015) Alexey Dosovitskiy, Philipp Fischer, Eddy Ilg, Philip Hausser, Caner Hazirbas, Vladimir Golkov, Patrick Van Der Smagt, Daniel Cremers, and Thomas Brox. Flownet: Learning optical flow with convolutional networks. In Proceedings of the IEEE international conference on computer vision, pages 2758–2766, 2015.

[bib.bib23] Eppenhof and Pluim (2018) Koen AJ Eppenhof and Josien PW Pluim. Pulmonary ct registration through supervised learning with convolutional neural networks. IEEE transactions on medical imaging, 38(5):1097–1105, 2018.

[bib.bib24] Fan et al. (2018) Jingfan Fan, Xiaohuan Cao, Zhong Xue, Pew-Thian Yap, and Dinggang Shen. Adversarial similarity network for evaluating image alignment in deep learning based registration. In International Conference on Medical Image Computing and Computer-Assisted Intervention, pages 739–746. Springer, 2018.

[bib.bib25] Fan et al. (2019) Jingfan Fan, Xiaohuan Cao, Pew-Thian Yap, and Dinggang Shen. Birnet: Brain image registration using dual-supervised fully convolutional networks. Medical image analysis, 54:193–206, 2019.

[bib.bib26] Fisch et al. (2021) Lukas Fisch, Ramona Leenings, Nils R. Winter, Udo Dannlowski, Christian Gaser, James H. Cole, and Tim Hahn. Editorial: Predicting chronological age from structural neuroimaging: The predictive analytics competition 2019. Frontiers in Psychiatry, 12, 2021. ISSN 1664-0640.

[bib.bib27] Fischl (2012) Bruce Fischl. Freesurfer. NeuroImage, 62(2):774–781, 2012.

[bib.bib28] Förstner and Gülch (1987) Wolfgang Förstner and Eberhard Gülch. A fast operator for detection and precise location of distinct points, corners and centres of circular features. In Proc. ISPRS intercommission conference on fast processing of photogrammetric data, pages 281–305. Interlaken, 1987.

[bib.bib29] Fowler et al. (2021) Christopher Fowler, Stephanie R. Rainey-Smith, Sabine Bird, J. Bomke, Pierrick Bourgeat, Belinda M. Brown, Samantha C. Burnham, Ashley I. Bush, Carly Chadunow, Steven Collins, et al. Fifteen years of the australian imaging, biomarkers and lifestyle (aibl) study: Progress and observations from 2,359 older adults spanning the spectrum from cognitive normality to alzheimer’s disease. Journal of Alzheimer’s Disease Reports, 5(1):443–468, Jun 2021. PMID: 34368630; PMCID: PMC8293663.

[bib.bib30] Frisken et al. (2020) Sarah Frisken, Ma Luo, Parikshit Juvekar, Adomas Bunevicius, Ines Machado, Prashin Unadkat, Melina M. Bertotti, Matt Toews, William M. Wells, Michael I. Miga, and Alexandra J. Golby. A comparison of thin-plate spline deformation and finite element modeling to compensate for brain shift during tumor resection. International Journal of Computer Assisted Radiology and Surgery, 15(1):75–85, 2020. . URL https://doi.org/10.1007/s11548-019-02057-2.

[bib.bib31] Gousias et al. (2012) Ioannis S. Gousias, A. David Edwards, Mary A. Rutherford, Serena J. Counsell, Joseph V. Hajnal, Daniel Rueckert, and Alexander Hammers. Magnetic resonance imaging of the newborn brain: manual segmentation of labelled atlases in term-born and preterm infants. Neuroimage, 62(3):1499–1509, Sep 2012. Epub 2012 Jun 17. PMID: 22713673.

[bib.bib32] Grøvik et al. (2020) Eirik Grøvik, Dong Yi, Michael Iv, Edward Tong, Daniel Rubin, and Greg Zaharchuk. Deep learning enables automatic detection and segmentation of brain metastases on multisequence mri. Journal of Magnetic Resonance Imaging, 51(1):175–182, Jan 2020. Epub 2019 May 2. PMID: 31050074; PMCID: PMC7199496.

[bib.bib33] Guyader et al. (2018) J. Guyader, Wyke Huizinga, D. Poot, Matthijs van Kranenburg, A. Uitterdijk, W. Niessen, and S. Klein. Groupwise image registration based on a total correlation dissimilarity measure for quantitative mri and dynamic imaging data. Scientific Reports, 8, 2018.

[bib.bib34] Harris et al. (1988) Christopher G Harris, Mike Stephens, et al. A combined corner and edge detector. In Alvey vision conference, volume 15, pages 10–5244. Citeseer, 1988.

[bib.bib35] Heinrich et al. (2012) Mattias P Heinrich, Mark Jenkinson, Manav Bhushan, Tahreema Matin, Fergus V Gleeson, Michael Brady, and Julia A Schnabel. Mind: Modality independent neighbourhood descriptor for multi-modal deformable registration. Medical image analysis, 16(7):1423–1435, 2012.

[bib.bib36] Hermosillo et al. (2002) Gerardo Hermosillo, Christophe Chefd’Hotel, and Olivier Faugeras. Variational methods for multimodal image matching. International Journal of Computer Vision, 50(3):329–343, 2002.

[bib.bib37] Hernandez Petzsche et al. (2022) M. R. Hernandez Petzsche, E. de la Rosa, U. Hanning, et al. Isles 2022: A multi-center magnetic resonance imaging stroke lesion segmentation dataset. Scientific Data, 9:762, 2022.

[bib.bib38] Hill et al. (2001) Derek LG Hill, Philipp G Batchelor, Mark Holden, and David J Hawkes. Medical image registration. Physics in medicine & biology, 46(3):R1, 2001.

[bib.bib39] Hoffmann et al. (2021) Malte Hoffmann, Benjamin Billot, Douglas N Greve, Juan Eugenio Iglesias, Bruce Fischl, and Adrian V Dalca. Synthmorph: learning contrast-invariant registration without acquired images. IEEE Transactions on Medical Imaging, 41(3):543–558, 2021.

[bib.bib40] Hoffmann et al. (2022) Malte Hoffmann, Benjamin Billot, Douglas N. Greve, Juan Eugenio Iglesias, Bruce Fischl, and Adrian V. Dalca. SynthMorph: Learning contrast-invariant registration without acquired images. IEEE Transactions on Medical Imaging, 41(3):543–558, mar 2022.

[bib.bib41] Hoopes et al. (2021) Andrew Hoopes, Malte Hoffmann, Bruce Fischl, John Guttag, and Adrian V. Dalca. Hypermorph: Amortized hyperparameter learning for image registration. IPMI, 2021.

[bib.bib42] Hu et al. (2018a) Yipeng Hu, Marc Modat, Eli Gibson, Nooshin Ghavami, Ester Bonmati, Caroline M Moore, Mark Emberton, J Alison Noble, Dean C Barratt, and Tom Vercauteren. Label-driven weakly-supervised learning for multimodal deformable image registration. In 2018 IEEE 15th International Symposium on Biomedical Imaging (ISBI 2018), pages 1070–1074. IEEE, 2018a.

[bib.bib43] Hu et al. (2018b) Yipeng Hu, Marc Modat, Eli Gibson, Wenqi Li, Nooshin Ghavami, Ester Bonmati, Guotai Wang, Steven Bandula, Caroline M Moore, Mark Emberton, et al. Weakly-supervised convolutional neural networks for multimodal image registration. Medical image analysis, 49:1–13, 2018b.

[bib.bib44] Iglesias (2023) Juan Eugenio Iglesias. A ready-to-use machine learning tool for symmetric multi-modality registration of brain mri. Scientific Reports, 13(1):6657, 2023. . URL https://doi.org/10.1038/s41598-023-33781-0.

[bib.bib45] Isensee et al. (2019) Fabian Isensee, Marianne Schell, Irada Pflueger, Gianluca Brugnara, David Bonekamp, Ulf Neuberger, Antje Wick, Heinz-Peter Schlemmer, Sabine Heiland, Wolfgang Wick, Martin Bendszus, Klaus H. Maier-Hein, and Philipp Kickingereder. Automated brain extraction of multisequence mri using artificial neural networks. Human Brain Mapping, 40(17):4952–4964, 2019.

[bib.bib46] Kazerooni et al. (2024) Anahita Fathi Kazerooni, Nastaran Khalili, Xinyang Liu, Debanjan Haldar, Zhifan Jiang, Syed Muhammed Anwar, Jake Albrecht, Maruf Adewole, Udunna Anazodo, Hannah Anderson, Sina Bagheri, Ujjwal Baid, Timothy Bergquist, Austin J. Borja, Evan Calabrese, Verena Chung, Gian-Marco Conte, Farouk Dako, James Eddy, Ivan Ezhov, Ariana Familiar, Keyvan Farahani, Shuvanjan Haldar, Juan Eugenio Iglesias, Anastasia Janas, Elaine Johansen, Blaise V Jones, Florian Kofler, Dominic LaBella, Hollie Anne Lai, Koen Van Leemput, Hongwei Bran Li, Nazanin Maleki, Aaron S McAllister, Zeke Meier, Bjoern Menze, Ahmed W Moawad, Khanak K Nandolia, Julija Pavaine, Marie Piraud, Tina Poussaint, Sanjay P Prabhu, Zachary Reitman, Andres Rodriguez, Jeffrey D Rudie, Mariana Sanchez-Montano, Ibraheem Salman Shaikh, Lubdha M. Shah, Nakul Sheth, Russel Taki Shinohara, Wenxin Tu, Karthik Viswanathan, Chunhao Wang, Jeffrey B Ware, Benedikt Wiestler, Walter Wiggins, Anna Zapaishchykova, Mariam Aboian, Miriam Bornhorst, Peter de Blank, Michelle Deutsch, Maryam Fouladi, Lindsey Hoffman, Benjamin Kann, Margot Lazow, Leonie Mikael, Ali Nabavizadeh, Roger Packer, Adam Resnick, Brian Rood, Arastoo Vossough, Spyridon Bakas, and Marius George Linguraru. The brain tumor segmentation (brats) challenge 2023: Focus on pediatrics (cbtn-connect-dipgr-asnr-miccai brats-peds), 2024.

[bib.bib47] Khan et al. (2021) Salman Hameed Khan, Muzammal Naseer, Munawar Hayat, Syed Waqas Zamir, F. Khan, and M. Shah. Transformers in vision: A survey. ACM Computing Surveys (CSUR), 54:1 – 41, 2021.

[bib.bib48] Kingma and Ba (2017) Diederik P. Kingma and Jimmy Ba. Adam: A method for stochastic optimization. arXiv preprint arXiv:1412.6980, 2017.

[bib.bib49] Konstantinos Ntatsis et al. (2023) Konstantinos Ntatsis, Niels Dekker, Viktor van der Valk, Tom Birdsong, Dženan Zukić, Stefan Klein, Marius Staring, and Matthew McCormick. itk-elastix: Medical image registration in Python. In Meghann Agarwal, Chris Calloway, and Dillon Niederhut, editors, Proceedings of the 22nd Python in Science Conference, pages 101 – 105, 2023.

[bib.bib50] Krebs et al. (2019) Julian Krebs, Hervé Delingette, Boris Mailhé, Nicholas Ayache, and Tommaso Mansi. Learning a probabilistic model for diffeomorphic registration. IEEE transactions on medical imaging, 38(9):2165–2176, 2019.

[bib.bib51] Kuijf et al. (2019) Hugo J. Kuijf, J. Matthijs Biesbroek, Jeroen De Bresser, Rutger Heinen, Simon Andermatt, Mariana Bento, Matt Berseth, Mikhail Belyaev, M. Jorge Cardoso, Adria Casamitjana, et al. Standardized assessment of automatic segmentation of white matter hyperintensities and results of the wmh segmentation challenge. IEEE Transactions on Medical Imaging, 38(11):2556–2568, Nov 2019. Epub 2019 Mar 19. PMID: 30908194; PMCID: PMC7590957.

[bib.bib52] LaMontagne et al. (2019) Pamela J. LaMontagne, Tammie LS. Benzinger, John C. Morris, Sarah Keefe, Russ Hornbeck, Chengjie Xiong, Elizabeth Grant, Jason Hassenstab, Krista Moulder, Andrei G. Vlassenko, Marcus E. Raichle, Carlos Cruchaga, and Daniel Marcus. Oasis-3: Longitudinal neuroimaging, clinical, and cognitive dataset for normal aging and alzheimer disease. medRxiv, 2019.

[bib.bib53] Lee et al. (2019a) Matthew C. H. Lee, Ozan Oktay, Andreas Schuh, Michiel Schaap, and Ben Glocker. Image-and-spatial transformer networks for structure-guided image registration, 2019a.

[bib.bib54] Lee et al. (2019b) Matthew CH Lee, Ozan Oktay, Andreas Schuh, Michiel Schaap, and Ben Glocker. Image-and-spatial transformer networks for structure-guided image registration. In International Conference on Medical Image Computing and Computer-Assisted Intervention, pages 337–345. Springer, 2019b.

[bib.bib55] Lenc and Vedaldi (2016) Karel Lenc and Andrea Vedaldi. Learning covariant feature detectors. In European conference on computer vision, pages 100–117. Springer, 2016.

[bib.bib56] Liu et al. (2021) Fengze Liu, Ke Yan, Adam Harrison, Dazhou Guo, Le Lu, Alan Yuille, Lingyun Huang, Guotong Xie, Jing Xiao, Xianghua Ye, and Dakai Jin. Same: Deformable image registration based on self-supervised anatomical embeddings, 2021.

[bib.bib57] Lowe (2004) David G Lowe. Distinctive image features from scale-invariant keypoints. International journal of computer vision, 60(2):91–110, 2004.

[bib.bib58] Ma et al. (2021) Jiayi Ma, Xingyu Jiang, Aoxiang Fan, Junjun Jiang, and Junchi Yan. Image matching from handcrafted to deep features: A survey. International Journal of Computer Vision, 129(1):23–79, 2021.

[bib.bib59] Ma et al. (2022) Mingrui Ma, Lei Song, Yuanbo Xu, and Gui-Xian Liu. Symmetric transformer-based network for unsupervised image registration. Knowl. Based Syst., 257:109959, 2022.

[bib.bib60] Ma et al. (2020) Tianyu Ma, Ajay Gupta, and Mert R Sabuncu. Volumetric landmark detection with a multi-scale shift equivariant neural network. International Symposium on Biomedical Imaging (ISBI), pages 981–985, 2020.

[bib.bib61] Machado et al. (2018) Inês Machado, Matthew Toews, Jie Luo, Prashin Unadkat, Walid Essayed, Elizabeth George, Pedro Teodoro, Herculano Carvalho, Jorge Martins, Polina Golland, Steve Pieper, Sarah Frisken, Alexandra Golby, and William Wells. Non-rigid registration of 3d ultrasound for neurosurgery using automatic feature detection and matching. International Journal of Computer Assisted Radiology and Surgery, 13(10):1525–1538, 2018. . URL https://doi.org/10.1007/s11548-018-1786-7.

[bib.bib62] Malinin et al. (2022) Andrey Malinin, Andreas Athanasopoulos, Muhamed Barakovic, Meritxell Bach Cuadra, Mark J. F. Gales, Cristina Granziera, Mara Graziani, Nikolay Kartashev, Konstantinos Kyriakopoulos, Po-Jui Lu, Nataliia Molchanova, Antonis Nikitakis, Vatsal Raina, Francesco La Rosa, Eli Sivena, Vasileios Tsarsitalidis, Efi Tsompopoulou, and Elena Volf. Shifts 2.0: Extending the dataset of real distributional shifts, 2022.

[bib.bib63] Marcus et al. (2007) Daniel S. Marcus, Tracy H. Wang, Jamie Parker, John G. Csernansky, John C. Morris, and Randy L. Buckner. Open Access Series of Imaging Studies (OASIS): Cross-sectional MRI Data in Young, Middle Aged, Nondemented, and Demented Older Adults. Journal of Cognitive Neuroscience, 19(9):1498–1507, 09 2007. ISSN 0898-929X.

[bib.bib64] Marcus et al. (2010) Daniel S. Marcus, Anthony F. Fotenos, John G. Csernansky, John C. Morris, and Randy L. Buckner. Open Access Series of Imaging Studies: Longitudinal MRI Data in Nondemented and Demented Older Adults. Journal of Cognitive Neuroscience, 22(12):2677–2684, 12 2010. ISSN 0898-929X.

[bib.bib65] Marek et al. (2011) Kenneth Marek, Danna Jennings, Shirley Lasch, Andrew Siderowf, Caroline Tanner, Tanya Simuni, Chris Coffey, Karl Kieburtz, Emily Flagg, Sohini Chowdhury, Werner Poewe, Brit Mollenhauer, Paracelsus-Elena Klinik, Todd Sherer, Mark Frasier, Claire Meunier, Alice Rudolph, Cindy Casaceli, John Seibyl, Susan Mendick, Norbert Schuff, Ying Zhang, Arthur Toga, Karen Crawford, Alison Ansbach, Pasquale De Blasio, Michele Piovella, John Trojanowski, Les Shaw, Andrew Singleton, Keith Hawkins, Jamie Eberling, Deborah Brooks, David Russell, Laura Leary, Stewart Factor, Barbara Sommerfeld, Penelope Hogarth, Emily Pighetti, Karen Williams, David Standaert, Stephanie Guthrie, Robert Hauser, Holly Delgado, Joseph Jankovic, Christine Hunter, Matthew Stern, Baochan Tran, Jim Leverenz, Marne Baca, Sam Frank, Cathi-Ann Thomas, Irene Richard, Cheryl Deeley, Linda Rees, Fabienne Sprenger, Elisabeth Lang, Holly Shill, Sanja Obradov, Hubert Fernandez, Adrienna Winters, Daniela Berg, Katharina Gauss, Douglas Galasko, Deborah Fontaine, Zoltan Mari, Melissa Gerstenhaber, David Brooks, Sophie Malloy, Paolo Barone, Katia Longo, Tom Comery, Bernard Ravina, Igor Grachev, Kim Gallagher, Michelle Collins, Katherine L. Widnell, Suzanne Ostrowizki, Paulo Fontoura, Tony Ho, Johan Luthman, Marcel van der Brug, Alastair D. Reith, and Peggy Taylor. The parkinson progression marker initiative (ppmi). Progress in Neurobiology, 95(4):629–635, 2011. ISSN 0301-0082. Biological Markers for Neurodegenerative Diseases.

[bib.bib66] Matas et al. (2004) Jiri Matas, Ondrej Chum, Martin Urban, and Tomás Pajdla. Robust wide-baseline stereo from maximally stable extremal regions. Image and vision computing, 22(10):761–767, 2004.

[bib.bib67] Mattes et al. (2003) David Mattes, David R Haynor, Hubert Vesselle, Thomas K Lewellen, and William Eubank. Pet-ct image registration in the chest using free-form deformations. IEEE transactions on medical imaging, 22(1):120–128, 2003.

[bib.bib68] Menze et al. (2015) Bjoern H. Menze, Andras Jakab, Stefan Bauer, Jayashree Kalpathy-Cramer, Keyvan Farahani, Justin Kirby, Yuliya Burren, Nicole Porz, Johannes Slotboom, Roland Wiest, Levente Lanczi, Elizabeth Gerstner, Marc-Andre Weber, Tal Arbel, Brian B. Avants, Nicholas Ayache, Patricia Buendia, D. Louis Collins, Nicolas Cordier, Jason J. Corso, Antonio Criminisi, Tilak Das, Herve Delingette, Cagatay Demiralp, Christopher R. Durst, Michel Dojat, Senan Doyle, Joana Festa, Florence Forbes, Ezequiel Geremia, Ben Glocker, Polina Golland, Xiaotao Guo, Andac Hamamci, Khan M. Iftekharuddin, Raj Jena, Nigel M. John, Ender Konukoglu, Danial Lashkari, José António Mariz, Raphael Meier, Sérgio Pereira, Doina Precup, Stephen J. Price, Tammy Riklin Raviv, Syed M. S. Reza, Michael Ryan, Duygu Sarikaya, Lawrence Schwartz, Hoo-Chang Shin, Jamie Shotton, Carlos A. Silva, Nuno Sousa, Nagesh K. Subbanna, Gabor Szekely, Thomas J. Taylor, Owen M. Thomas, Nicholas J. Tustison, Gozde Unal, Flor Vasseur, Max Wintermark, Dong Hye Ye, Liang Zhao, Binsheng Zhao, Darko Zikic, Marcel Prastawa, Mauricio Reyes, and Koen Van Leemput. The multimodal brain tumor image segmentation benchmark (brats). IEEE Transactions on Medical Imaging, 34(10):1993–2024, 2015.

[bib.bib69] Montesinos et al. (1998) Philippe Montesinos, Valérie Gouet, and Rachid Deriche. Differential invariants for color images. In Proceedings. Fourteenth International Conference on Pattern Recognition (Cat. No. 98EX170), volume 1, pages 838–840. IEEE, 1998.

[bib.bib70] Moyer et al. (2021) Daniel Moyer, Esra Abaci Turk, P Ellen Grant, William M Wells, and Polina Golland. Equivariant filters for efficient tracking in 3d imaging. In Medical Image Computing and Computer Assisted Intervention–MICCAI 2021: 24th International Conference, Strasbourg, France, September 27–October 1, 2021, Proceedings, Part IV 24, pages 193–202. Springer, 2021.

[bib.bib71] Muslim et al. (2022) A.M. Muslim, S. Mashohor, G.A. Gawwam, R. Mahmud, M.B. Hanafi, O. Alnuaimi, R. Josephine, and A.D. Almutairi. Brain mri dataset of multiple sclerosis with consensus manual lesion segmentation and patient meta information. Data Brief, 42:108139, Apr 2022.

[bib.bib72] Oliveira and Tavares (2014) Francisco PM Oliveira and Joao Manuel RS Tavares. Medical image registration: a review. Computer methods in biomechanics and biomedical engineering, 17(2):73–93, 2014.

[bib.bib73] Ono et al. (2018) Yuki Ono, Eduard Trulls, Pascal Fua, and Kwang Moo Yi. Lf-net: Learning local features from images. arXiv preprint arXiv:1805.09662, 2018.

[bib.bib74] Pérez-García et al. (2020) Fernando Pérez-García, Roman Rodionov, Ali Alim-Marvasti, Rachel Sparks, John S. Duncan, and Sébastien Ourselin. Simulation of brain resection for cavity segmentation using self-supervised and semi-supervised learning. In Anne L. Martel, Purang Abolmaesumi, Danail Stoyanov, Diana Mateus, Maria A. Zuluaga, S. Kevin Zhou, Daniel Racoceanu, and Leo Joskowicz, editors, Medical Image Computing and Computer Assisted Intervention – MICCAI 2020, pages 115–125, Cham, 2020. Springer International Publishing. ISBN 978-3-030-59716-0.

[bib.bib75] Petersen et al. (2010) Ronald C. Petersen, Paul S. Aisen, Laurel A. Beckett, Michael C. Donohue, Anthony C. Gamst, Danielle J. Harvey, Clifford R. Jr Jack, William J. Jagust, Leslie M. Shaw, Arthur W. Toga, John Q. Trojanowski, and Michael W. Weiner. Alzheimer’s disease neuroimaging initiative (adni): clinical characterization. Neurology, 74(3):201–209, Jan 2010. Epub 2009 Dec 30. PMID: 20042704; PMCID: PMC2809036.

[bib.bib76] Qin et al. (2019) Chen Qin, Bibo Shi, Rui Liao, Tommaso Mansi, Daniel Rueckert, and Ali Kamen. Unsupervised deformable registration for multi-modal images via disentangled representations. Lecture Notes in Computer Science Information Processing in Medical Imaging, page 249–261, 2019.

[bib.bib77] Reuter et al. (2010) Martin Reuter, H. Diana Rosas, and Bruce Fischl. Highly accurate inverse consistent registration: a robust approach. Neuroimage, 53(4):1181–1196, Dec 2010. Epub 2010 Jul 14. PMID: 20637289; PMCID: PMC2946852.

[bib.bib78] Rohr et al. (2001) K. Rohr, H.S. Stiehl, R. Sprengel, T.M. Buzug, J. Weese, and M.H. Kuhn. Landmark-based elastic registration using approximating thin-plate splines. IEEE Transactions on Medical Imaging, 20(6):526–534, 2001.

[bib.bib79] Rosenfeld and Thurston (1971) Azriel Rosenfeld and Mark Thurston. Edge and curve detection for visual scene analysis. IEEE Transactions on computers, 100(5):562–569, 1971.

[bib.bib80] Rudie et al. (2022) Jeffrey D. Rudie, Evan Calabrese, Rachit Saluja, David Weiss, John B. Colby, Soonmee Cha, Christopher P. Hess, Andreas M. Rauschecker, Leo P. Sugrue, and Javier E. Villanueva-Meyer. Longitudinal assessment of posttreatment diffuse glioma tissue volumes with three-dimensional convolutional neural networks. Radiology: Artificial Intelligence, 4(5):e210243, 2022.

[bib.bib81] Rudie et al. (2024) Jeffrey D. Rudie, Rachit Saluja, David A. Weiss, Pierre Nedelec, Evan Calabrese, John B. Colby, Benjamin Laguna, John Mongan, Steve Braunstein, Christopher P. Hess, Andreas M. Rauschecker, Leo P. Sugrue, and Javier E. Villanueva-Meyer. The university of california san francisco brain metastases stereotactic radiosurgery (ucsf-bmsr) mri dataset. Radiology: Artificial Intelligence, 6(2):e230126, 2024.

[bib.bib82] Sofka et al. (2017) Michal Sofka, Fausto Milletari, Jimmy Jia, and Alex Rothberg. Fully convolutional regression network for accurate detection of measurement points. In Deep learning in medical image analysis and multimodal learning for clinical decision support, pages 258–266. Springer, 2017.

[bib.bib83] Song et al. (2022) Xinrui Song, Hanqing Chao, Xuanang Xu, Hengtao Guo, Sheng Xu, Baris Turkbey, Bradford J. Wood, Thomas Sanford, Ge Wang, and Pingkun Yan. Cross-modal attention for multi-modal image registration. Medical Image Analysis, 82:102612, 2022. ISSN 1361-8415.

[bib.bib84] Sotiras et al. (2013) Aristeidis Sotiras, Christos Davatzikos, and Nikos Paragios. Deformable medical image registration: A survey. IEEE Transactions on Medical Imaging, 32(7):1153–1190, 2013.

[bib.bib85] Tang et al. (2023) Canhui Tang, Yiheng Li, S. Du, Guofa Wang, and Zhiqiang Tian. Hd2reg: Hierarchical descriptors and detectors for point cloud registration. 2023 IEEE Intelligent Vehicles Symposium (IV), pages 1–6, 2023.

[bib.bib86] Tang et al. (2019) Jiexiong Tang, Hanme Kim, V. Guizilini, Sudeep Pillai, and Rares Ambrus. Neural outlier rejection for self-supervised keypoint learning. ArXiv, abs/1912.10615, 2019.

[bib.bib87] Toews et al. (2013a) Matthew Toews, Lilla Zöllei, and William M Wells. Feature-based alignment of volumetric multi-modal images. In International Conference on Information Processing in Medical Imaging, pages 25–36. Springer, 2013a.

[bib.bib88] Toews et al. (2013b) Matthew Toews, Lilla Zöllei, and William M. Wells. Feature-based alignment of volumetric multi-modal images. In James C. Gee, Sarang Joshi, Kilian M. Pohl, William M. Wells, and Lilla Zöllei, editors, Information Processing in Medical Imaging, pages 25–36, Berlin, Heidelberg, 2013b. Springer Berlin Heidelberg. ISBN 978-3-642-38868-2.

[bib.bib89] Tuytelaars and Mikolajczyk (2008) Tinne Tuytelaars and Krystian Mikolajczyk. Local invariant feature detectors: a survey. Now Publishers Inc, 2008.

[bib.bib90] Uludağ and Roebroeck (2014) Kâmil Uludağ and Alard Roebroeck. General overview on the merits of multimodal neuroimaging data fusion. Neuroimage, 102:3–10, 2014.

[bib.bib91] Ulyanov et al. (2016) Dmitry Ulyanov, Andrea Vedaldi, and Victor Lempitsky. Instance normalization: The missing ingredient for fast stylization. arXiv preprint arXiv:1607.08022, 2016.

[bib.bib92] Uzunova et al. (2017) Hristina Uzunova, Matthias Wilms, Heinz Handels, and Jan Ehrhardt. Training cnns for image registration from few samples with model-based data augmentation. In International Conference on Medical Image Computing and Computer-Assisted Intervention, pages 223–231. Springer, 2017.

[bib.bib93] Van de Weijer et al. (2005) Joost Van de Weijer, Theo Gevers, and Andrew D Bagdanov. Boosting color saliency in image feature detection. IEEE transactions on pattern analysis and machine intelligence, 28(1):150–156, 2005.

[bib.bib94] Verdie et al. (2015) Yannick Verdie, Kwang Yi, Pascal Fua, and Vincent Lepetit. Tilde: A temporally invariant learned detector. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 5279–5288, 2015.

[bib.bib95] Viklands (2006) T. Viklands. Algorithms for the weighted orthogonal procrustes problem and other least squares problems, 2006.

[bib.bib96] Viola and Wells III (1997) Paul Viola and William M Wells III. Alignment by maximization of mutual information. International journal of computer vision, 24(2):137–154, 1997.

[bib.bib97] Wachinger et al. (2018) Christian Wachinger, Matthew Toews, Georg Langs, William Wells, and Polina Golland. Keypoint transfer for fast whole-body segmentation. IEEE transactions on medical imaging, 39(2):273–282, 2018.

[bib.bib98] Wang et al. (2023) Alan Q. Wang, Evan M. Yu, Adrian V. Dalca, and Mert R. Sabuncu. A robust and interpretable deep learning framework for multi-modal registration via keypoints. Medical Image Analysis, 90:102962, 2023. ISSN 1361-8415.

[bib.bib99] Wu et al. (2015) Guorong Wu, Minjeong Kim, Qian Wang, Brent C Munsell, and Dinggang Shen. Scalable high-performance image registration framework by unsupervised deep feature representations learning. IEEE Transactions on Biomedical Engineering, 63(7):1505–1516, 2015.

[bib.bib100] Yang et al. (2017) Xiao Yang, Roland Kwitt, Martin Styner, and Marc Niethammer. Quicksilver: Fast predictive image registration–a deep learning approach. NeuroImage, 158:378–396, 2017.

[bib.bib101] Yi et al. (2016) Kwang Moo Yi, Eduard Trulls, Vincent Lepetit, and Pascal Fua. Lift: Learned invariant feature transform. In European conference on computer vision, pages 467–483. Springer, 2016.

[bib.bib102] Yi et al. (2018) Kwang Moo Yi, Eduard Trulls, Yuki Ono, Vincent Lepetit, Mathieu Salzmann, and Pascal Fua. Learning to find good correspondences, 2018.